题目内容
已知函数f(x)=mxlnx(m>0),f(x)在点(e,f(e))处的切线与x轴、y轴分别交于A、B两点,且△AOB的面积为
,证明:当x>e时,对于任意正实数t不等式f(x+t)<f(x)et恒成立.
| e2 |
| 4 |
考点:利用导数研究曲线上某点切线方程
专题:导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:求出函数f(x)的导数,求得切线的斜率,得到切线方程,分别令x=0,y=0,得到y,x轴上的截距,再由三角形的面积公式,可得m=1,将不等式转化为
<
,即证当x>e,对于任意正实数t恒成立,构造函数g(x)=
,利用导数研究函数的单调性即可得到结论.
| f(x+t) |
| ex+t |
| f(x) |
| ex |
| f(x) |
| ex |
解答:
证明:f(x)=mxlnx(m>0)的导数为f′(x)=m(lnx+1),
在点(e,f(e))处的切线斜率为f′(e)=2m,
切点为(e,me),
则在点(e,f(e))处的切线方程为y-me=2m(x-e),
即为y=2mx-me,
令x=0可得y=-me,令y=0可得x=
.
即有
•
•me=
,解得m=1,
即有f(x)=xlnx.
不等式f(x+t)<f(x)et可转化为f(t+x)<f(x)e(t+x-x),
即证
<
,当x>e,对于任意正实数t恒成立.
设g(x)=
,
则g′(x)=
,
令h(x)=lnx+1-xlnx,h′(x)=
-lnx-1,h″(x)=-
-
<0,(x>e)
故h'(x)在(e,+∞)上单减,又h'(e)=
-2<0,
即有h′(x)<h′(e)<0,即h(x)在x>e上递减,
即有h(x)<h(e)=2-e<0,即为g′(x)<0,g(x)在x>e上递减.
由x>e时,对于任意正实数t,x+t>x,
则有g(x+t)>g(x),
即有不等式f(x+t)<f(x)et恒成立.
在点(e,f(e))处的切线斜率为f′(e)=2m,
切点为(e,me),
则在点(e,f(e))处的切线方程为y-me=2m(x-e),
即为y=2mx-me,
令x=0可得y=-me,令y=0可得x=
| e |
| 2 |
即有
| 1 |
| 2 |
| e |
| 2 |
| e2 |
| 4 |
即有f(x)=xlnx.
不等式f(x+t)<f(x)et可转化为f(t+x)<f(x)e(t+x-x),
即证
| f(x+t) |
| ex+t |
| f(x) |
| ex |
设g(x)=
| f(x) |
| ex |
则g′(x)=
| lnx+1-xlnx |
| ex |
令h(x)=lnx+1-xlnx,h′(x)=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
故h'(x)在(e,+∞)上单减,又h'(e)=
| 1 |
| e |
即有h′(x)<h′(e)<0,即h(x)在x>e上递减,
即有h(x)<h(e)=2-e<0,即为g′(x)<0,g(x)在x>e上递减.
由x>e时,对于任意正实数t,x+t>x,
则有g(x+t)>g(x),
即有不等式f(x+t)<f(x)et恒成立.
点评:本题考查导数的运用:求切线方程和判断单调性,主要考查不等式恒成立的证明,利用条件将不等式进行转换,构造函数是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
当x∈[1,5]时,函数f(x)=3x2-4x+c的值域为( )
| A、[f(1),f(5)] | ||
B、[f(1),f(
| ||
C、[f(
| ||
| D、[c,f(5)] |
 如图所示为M与N两点间的电路,在时间T内不同元件发生故障的事件是互相独立的,它们发生故障的概率如下表所示:
如图所示为M与N两点间的电路,在时间T内不同元件发生故障的事件是互相独立的,它们发生故障的概率如下表所示: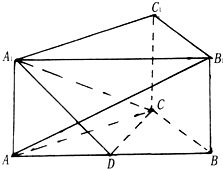 如图所示,在直三棱柱ABC-A1B1C1中,AA1=2,AB=4,AC=BC=3,D为AB的中点,且AB1⊥A1C
如图所示,在直三棱柱ABC-A1B1C1中,AA1=2,AB=4,AC=BC=3,D为AB的中点,且AB1⊥A1C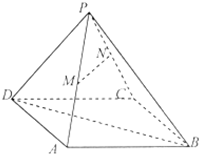 如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2
如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2