Question

椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的右焦点为F，A为OF的中点，P为椭圆C上的一点，以AP为直径的圆过点F且与y轴相切．则椭圆C的离心率为

 

．

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：先建立直角坐标系，设出F坐标，然后由AP为直径得PF垂直与x轴求出P，再求直径|AP|长和圆心坐标，由圆与y轴相切，求出半径r，利用|AP|=2r做构造含有a，b，c等式，再由椭圆b²=a²-c²消去b，转为e=

c

a

求解．

解答： 解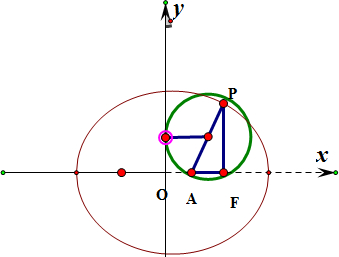：由题意做出图如右，设椭圆的焦距为2c（c＞0），则右焦点F（c，O），A（

c

2

，0）
以AP为直径的圆过点F，则∠AFP=90°，即PF垂直与x轴，P为椭圆上点，则P（c，

b2

a

）
直径|AP|=

(c- c 2 )2-( b2 a )2

 ，且圆心为AP中点，有中点坐标公式可求得（

3

4

c，

b2

2a

）
又由题意圆与y轴相切得圆心到y轴的距离等于半径，即圆的半径r=

3

4

c，
则|AP|=2r，即

(c- c 2 )2-( b2 a )2

 =

3

2

c，代入b²=a²-c²化简得a²-c²-

2

ac=0，
同除以a²得（

c

a

）²+

2

c

a

-1=0，
又椭圆离心率e=

c

a

（0＜e＜1），
得e²+

2

e-1=0，
解得e=

6 - 2

2

．
故答案为：

6 - 2

2

．

点评：本题考察椭圆的离心率的求法，基本上都是利用题目条件构造构造含有a，b，c等式，再由椭圆b²=a²-c²消去b，转为e=

c

a

求解．