题目内容
已知函数f(x)在区间[0,+∞)上单调递减:则满足f(x2+2x+3)<f(6)的实数x的取值范围为( )
| A、(-∞,-3)∪(1,+∞) |
| B、(-3,1) |
| C、(-∞,-3) |
| D、(1,+∞) |
考点:函数单调性的性质
专题:函数的性质及应用,不等式的解法及应用
分析:由函数f(x)在区间[0,+∞)上单调递减,可将不等式f(x2+2x+3)<f(6)化为x2+2x+3>6,解二次不等式可得答案.
解答:
解:∵函数f(x)在区间[0,+∞)上单调递减,
若f(x2+2x+3)<f(6),
则x2+2x+3>6,
即x2+2x-3>0,
解得x∈(-∞,-3)∪(1,+∞),
故实数x的取值范围为(-∞,-3)∪(1,+∞),
故选:A.
若f(x2+2x+3)<f(6),
则x2+2x+3>6,
即x2+2x-3>0,
解得x∈(-∞,-3)∪(1,+∞),
故实数x的取值范围为(-∞,-3)∪(1,+∞),
故选:A.
点评:本题考查的知识点是函数单调性的性质,一元二次不等式的解法,其中根据函数的单调性,将原不等式化为x2+2x+3>6,是解答的关键.

练习册系列答案
相关题目
已知a、b∈R,a+bi是虚数的充分必要条件是( )
| A、ab≠0 | B、a≠0 |
| C、b≠0 | D、a=0且b≠0 |
与角-
终边相同的角是( )
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tanα=-
,sinβ=
,β∈(
,π),则tan(2α-β)=( )
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知a=log1.20.3,b=log1.20.8,c=1.50.5,则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
“-3<m<-1”是方程
+
=1表示双曲线的( )
| x2 |
| 2+m |
| y2 |
| m+1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
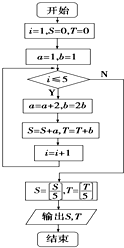 阅读程序框图设[x]表示取x的整数部分,如[5]=5,[2.7]=2,经过程序框图运行后输出结果为S,T,设z1=S-Ti,z2=1+i,z=z1•z2,则|z|=
阅读程序框图设[x]表示取x的整数部分,如[5]=5,[2.7]=2,经过程序框图运行后输出结果为S,T,设z1=S-Ti,z2=1+i,z=z1•z2,则|z|=