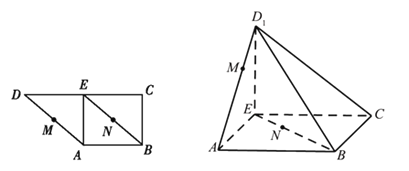
题目内容
【题目】已知空间中两条直线![]() ,
,![]() 所成的角为
所成的角为![]() ,
,![]() 为空间中给定的一个定点,直线
为空间中给定的一个定点,直线![]() 过点
过点![]() 且与直线
且与直线![]() 和直线
和直线![]() 所成的角都是
所成的角都是![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
A.当![]() 时,满足题意的直线
时,满足题意的直线![]() 不存在
不存在
B.当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且仅有1条
有且仅有1条
C.当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且仅有2条
有且仅有2条
D.当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且仅有3条
有且仅有3条
【答案】ABC
【解析】
为了讨论:过点![]() 与
与![]()
![]() 所成的角都是
所成的角都是![]() 的直线
的直线![]() 有且仅有几条,先将涉及到的线放置在同一个平面内观察,只须考虑过点
有且仅有几条,先将涉及到的线放置在同一个平面内观察,只须考虑过点![]() 与直线
与直线![]()
![]() 所成的角都是
所成的角都是![]() 的直线
的直线![]() 有且仅有几条即可,再利用
有且仅有几条即可,再利用![]() .进行角之间的大小比较即得.
.进行角之间的大小比较即得.
过点![]() 作
作![]() ,
,![]() ,则相交直线
,则相交直线![]()
![]() 确定一平面
确定一平面![]() .
.![]() 与
与![]() 夹角为
夹角为![]() 或
或![]() ,
,
设直线![]() 与
与![]()
![]() 均为
均为![]() 角,
角,
作![]() 面
面![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
记![]() ,
,![]() 或
或![]() ,则有
,则有![]() .
.
因为![]() ,所以
,所以![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() ;
;
当![]() 时,由
时,由![]() ,得
,得![]() .
.
故当![]() 时,直线
时,直线![]() 不存在;
不存在;
当![]() 时,直线
时,直线![]() 有且仅有1条;
有且仅有1条;
当![]() 时,直线
时,直线![]() 有且仅有2条;
有且仅有2条;
当![]() 时,直线
时,直线![]() 有且仅有3条;
有且仅有3条;
当![]() 时,直线
时,直线![]() 有且仅有4条;
有且仅有4条;
当![]() 时,直线
时,直线![]() 有且仅有1条.
有且仅有1条.
故![]() ,
,![]() ,
,![]() 均正确,
均正确,![]() 错误.
错误.
故选:![]() .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目