题目内容
若命题“?x>0,x+
≥t”为真,则实数t的取值范围为 .
| 9 |
| x+1 |
考点:全称命题
专题:函数的性质及应用
分析:由题意x+1>0,得x+
=(x+1)+
-1≥2
-1,即求出t的取值范围.
| 9 |
| x+1 |
| 9 |
| x+1 |
(x+1)•
|
解答:
解:∵命题“?x>0,x+
≥t”为真,
∴x+1>0,
∴x+
=(x+1)+
-1≥2
-1=5,
当且仅当x=2时,“=”成立;
∴t≤5,
即实数t的取值范围是(-∞,5].
故答案为:(-∞,5].
| 9 |
| x+1 |
∴x+1>0,
∴x+
| 9 |
| x+1 |
| 9 |
| x+1 |
(x+1)•
|
当且仅当x=2时,“=”成立;
∴t≤5,
即实数t的取值范围是(-∞,5].
故答案为:(-∞,5].
点评:本题考查了基本不等式的应用问题,解题时应根据题意,利用基本不等式a+b≥2
(a>0,b>0)来解答,是基础题.
| ab |

练习册系列答案
相关题目
若p或q为真,¬p为真,则( )
| A、p真q假 | B、p假q真 |
| C、p真q真 | D、p假q假 |
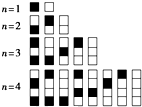 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当n=8时,黑色正方形互不相邻的着色方案共有
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当n=8时,黑色正方形互不相邻的着色方案共有