题目内容
1．在△ABC中，AB=2，BC=$\sqrt{10}$，cosA=$\frac{1}{4}$，则AB边上的高等于（ ）| A． | $\frac{3\sqrt{15}}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{3\sqrt{15}}{2}$ | D． | 3 |
分析 利用余弦定理求得丨AC丨，sinA=$\sqrt{1-cosA}$，则sinA=$\frac{丨CD丨}{丨AC丨}$，即可求得AB边上的高．
解答 解：在△ABC中，由余弦定理可知：丨BC丨2=丨AB丨2+丨AC丨2-2丨AB丨丨AC丨cosA，
整理得：丨AC丨2-丨AC丨-6=0，解得：丨AC丨=3，
sinA=$\sqrt{1-cosA}$=$\frac{\sqrt{15}}{4}$，
AB边上的高CD，
sinA=$\frac{丨CD丨}{丨AC丨}$，则丨CD丨=丨AC丨sinA=$\frac{3\sqrt{15}}{4}$
故选A．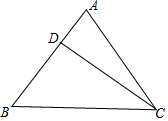
点评 本题考查余弦定理的应用，同角三角函数的基本关系，考查计算能力，属于基础题．
练习册系列答案
相关题目
9．设θ是第四象限角，则点P（sin（sinθ），cos（sinθ））在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右顶点A作斜率为-1的直线l，该直线与双曲线的两条渐近线的交点分别为B，C，若$\overrightarrow{AB}=\frac{1}{2}\overrightarrow{BC}$，则此双曲线的离心率是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
6．设?x?表示不小于实数x的最小整数，如?2.6?=3，?-3.5?=-3．已知函数f（x）=?x?2-2?x?，若函数F（x）=f（x）-k（x-2）+2在（-1，4]上有2个零点，则k的取值范围是（ ）
| A． | $[{-\frac{5}{2}，-1}）∪[2，5）$ | B． | $[{-1，-\frac{2}{3}}）∪[5，10）$ | C． | $（{-\frac{4}{3}，-1}]∪[5，10）$ | D． | $[{-\frac{4}{3}，-1}]∪[5，10）$ |
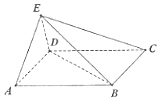如图所示，在四棱锥E-ABCD中，ABCD是边长为2的正方形，且AE⊥平面CDE，且∠DAE=30°