题目内容
12.已知函数f(x)=(lnx)ln(1-x).(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)求证:①lnx>$\frac{x-1}{{\sqrt{x}}}$;
②曲线y=f(x)上的所有点都落在圆$C:{(x-\frac{1}{2})^2}+{y^2}=\frac{1}{4}$内.
分析 (Ⅰ)求出f(x)的导数,根据函数的单调性求出函数的单调区间即可;
(Ⅱ)①构造函数φ(x),根据函数的单调性证明即可;
②结合①求出0<lnx•ln(1-x)<$\sqrt{x(1-x)}$,结合不等式的性质判断即可.
解答 解:(Ⅰ)函数的定义域为(0,1),由于f(1-x)=f(x),
故只需要考虑$x∈(0,\frac{1}{2})$的单调性 (1分)
$f'(x)=\frac{ln(1-x)}{x}-\frac{lnx}{1-x}=\frac{1}{1-x}[{\frac{1-x}{x}ln(1-x)-lnx}]$(2分)
令$g(x)=\frac{1-x}{x}ln(1-x)-lnx$则$g'(x)=-\frac{ln(1-x)+2x}{x^2}$(3分)
再令h(x)=ln(1-x)+2x则$h'(x)=2-\frac{1}{1-x}=\frac{1-2x}{1-x}$(4分)
当$x∈(0,\frac{1}{2})$时,h'(x)>0,则h(x)单调递增,又h(0)=0,∴h(x)>h(0)=0
则g'(x)<0∴g(x)单调递减∴$g(x)>g(\frac{1}{2})=0$∴f'(x)>0
∴f(x)的单调递增区间为$(0,\frac{1}{2})$,单调递减区间为$(\frac{1}{2},1)$(6分)
(Ⅱ)①令$φ(x)=lnx-\frac{x-1}{{\sqrt{x}}}=lnx-\sqrt{x}+\frac{1}{{\sqrt{x}}}(0<x<1)$,
$φ'(x)=\frac{1}{x}-\frac{1}{{2\sqrt{x}}}-\frac{1}{{2x\sqrt{x}}}=\frac{{-{{(\sqrt{x}-1)}^2}}}{{2x\sqrt{x}}}<0$
则φ(x)在(0,1)单调递减,
∴φ(x)>φ(1)=0即$lnx>\frac{x-1}{{\sqrt{x}}}$(9分)
②由①得$-lnx<\frac{1-x}{{\sqrt{x}}}⇒-ln(1-x)<\frac{x}{{\sqrt{1-x}}}$
∴$0<(lnx)ln(1-x)<\sqrt{x(1-x)}$
∴${(x-\frac{1}{2})^2}+{y^2}={(x-\frac{1}{2})^2}+{[{(lnx)ln(1-x)}]^2}<{(x-\frac{1}{2})^2}+x(1-x)=\frac{1}{4}$,
故曲线y=f(x)上的所有点都落在圆$C:{(x-\frac{1}{2})^2}+{y^2}=\frac{1}{4}$内. (12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及转化思想,不等式的性质,是一道中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
| 份(x) | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 水上狂欢节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
(2)旅游部门统计在每届水上狂欢节期间,每位外地游客可为本市增加100元左右的旅游收入,利用(1)中的线性回归方程,预测2017年第7届柳州国际水上狂欢节期间外地游客可为本市增加的旅游收入达多少?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
| A. | ∅ | B. | (3,4) | C. | (-2,1) | D. | (4,+∞) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
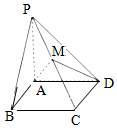 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.