题目内容
2.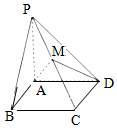 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.(1)在图中作出平面ADM与PB的交点N,并指出点N所在位置(不要求给出理由);
(2)求平面ADM将四棱锥P-ABCD分成上下两部分的体积比.
分析 (1)设N为PB中点,利用三角形中位线定理及其线面平行的判定定理可得截面如图所示.
(2)MN是△PBC的中位线,BC=1,可得MN=$\frac{1}{2}$,AN=$\frac{\sqrt{5}}{2}$,且AN⊥AD,利用梯形面积计算公式及其体积计算公式可得四棱锥P-ADMN的体积V1.而四棱锥P-ABCD的体积V,可得四棱锥被截下部分体积V2=V-V1.
解答 解:(1)设N为PB中点,截面如图所示.
(2)∵MN是△PBC的中位线,BC=1,
∴MN=$\frac{1}{2}$,AN=$\frac{\sqrt{5}}{2}$,且AN⊥AD,
∴梯形ADMN的面积为$\frac{1}{2}×(\frac{1}{2}+1)×\frac{\sqrt{5}}{2}$=$\frac{3\sqrt{5}}{8}$,
P点到截面ADMN的距离为P到直线AN的距离d=$\frac{2}{\sqrt{5}}$,
∴四棱锥P-ADMN的体积V1=$\frac{1}{3}×\frac{3\sqrt{5}}{8}×\frac{2}{\sqrt{5}}$=$\frac{1}{4}$,
而四棱锥P-ABCD的体积V=$\frac{1}{3}×2×1$=$\frac{2}{3}$,
所以四棱锥被截下部分体积V2=V-V1=$\frac{2}{3}-\frac{1}{4}$=$\frac{5}{12}$,
故上,下两部分体积比$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{5}$.
点评 本题以四棱锥为载体、线面平行的判定定理、三角形中位线定理、体积计算公式,考查学生的空间想象能力、推理论证能力和运算求解能力,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
13.已知直线l的极坐标方程为2ρsin(θ-$\frac{π}{4}$)=$\sqrt{2}$,点A的极坐标为(2$\sqrt{2}$,$\frac{7π}{4}$),则点A到直线l的距离为( )
| A. | $\frac{5}{3}\sqrt{3}$ | B. | $\frac{5}{2}\sqrt{3}$ | C. | $\frac{5}{3}\sqrt{2}$ | D. | $\frac{5}{2}\sqrt{2}$ |
17.双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点分别为F1,F2,P为右支上一点,且|$\overrightarrow{{PF}_{1}}$|=8,$\overrightarrow{{PF}_{1}}$•$\overrightarrow{{PF}_{2}}$=0,则双曲线的离心率为( )
| A. | 3 | B. | 5 | C. | $\sqrt{26}$ | D. | $\frac{5}{4}$ |
11.不等式-x2+4x-4<0的解集为( )
| A. | R | B. | Φ | C. | (-∞,2)∪(2,+∞) | D. | {2} |
