题目内容
15.若对?x∈[0,+∞),不等式2ax≤ex-1恒成立,则实数a的最大值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | 2 |
分析 对?x∈[0,+∞),不等式2ax≤ex-1恒成立,
等价于函数y=2ax的图象始终在函数y=ex-1图象的下方,其中x≥0;
在同一坐标系中画出函数y=2ax和y=ex-1的图象,结合图象求出a的最大值.
解答 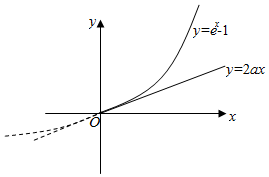 解:对?x∈[0,+∞),不等式2ax≤ex-1恒成立,
解:对?x∈[0,+∞),不等式2ax≤ex-1恒成立,
设y=2ax,y=ex-1,其中x≥0;
在同一坐标系中画出函数y=2ax和y=ex-1的图象如图所示;
则y′=ex,令x=0,得k=e0=1;
∴曲线y=ex-1过点O(0,0)的切线斜率为k=1;
根据题意得2a≤1,解得a≤$\frac{1}{2}$,
∴a的最大值为$\frac{1}{2}$.
故选:A.
点评 本题考查了不等式恒成立问题,解题时应用数形结合法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如表:
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
| 年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
20.从1,2,3,…,9这九个整数中同时取四个不同的数,其和为偶数,则不同取法共有( )
| A. | 62 | B. | 64 | C. | 65 | D. | 66 |
16.已知x,y均为正数,且x+y=2,则x+4$\sqrt{xy}$+4y的最大值是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
 如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒.
如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒.