题目内容
6.由曲线y=$\sqrt{x}$+1和直线x-2y+2=0所围成图形的面积为a,则二项式(x2-$\frac{2}{x}$)3a的展开式中含x-1的项的系数为( )| A. | 32 | B. | -32 | C. | 48 | D. | -48 |
分析 先利用定积分的意义求得a的值,再求出二项式展开式的通项公式,再令x的幂指数等于0-1,求得r的值,即可求得展开式中的含x-1的项的系数.
解答 解:由$\left\{\begin{array}{l}{y=\sqrt{x}+1}\\{y=\frac{1}{2}x+1}\end{array}\right.$ 求得x=0或 x=4,曲线y=$\sqrt{x}$+1和直线x-2y+2=0所围成图形的面积,
为a=${∫}_{0}^{4}$($\sqrt{x}$+1-$\frac{1}{2}$x-1)dx=($\frac{2}{3}$•${x}^{\frac{3}{2}}$-$\frac{1}{4}$•x2)${|}_{0}^{4}$=$\frac{2}{3}$•$\sqrt{64}$-4=$\frac{4}{3}$,
二项式(x2-$\frac{2}{x}$)3a =(x2-$\frac{2}{x}$)4的展开式的通项公式为Tr+1=${C}_{4}^{r}$•(-2)r•x8-3r,令8-3r=-1,求得r=3,
故展开式中含x-1的项的系数为-${C}_{4}^{3}$•8=-32,
故选:B.
点评 本题主要考查定积分的意义,二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.若a=$\frac{1-cosα}{sinα}$,b=$\frac{1+cosα}{sinα}$,则ab的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{2}$ |
14.已知函数g(x)=($\frac{1}{2}$)|x-1|,则r=g(2-0.1),s=g(log0.23),t=g(2),则r,s,t的大小关系是( )
| A. | t<r<s | B. | t<s<r | C. | s<r<t | D. | s<t<r |
15.(1-$\frac{1}{a}$)8的展开式中第7项是( )
| A. | $\frac{8}{{a}^{6}}$ | B. | -$\frac{8}{{a}^{6}}$ | C. | $\frac{56}{{a}^{6}}$ | D. | -$\frac{56}{{a}^{6}}$ |
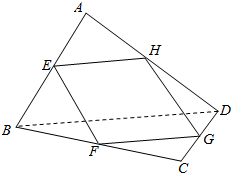 已知:空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.求证:E、F、G、H四点共面(如图所示)
已知:空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.求证:E、F、G、H四点共面(如图所示)