题目内容
5.等差数列{an}的前n项和为Sn,且a4=16,a10=8,则S13为156.分析 由已知条件等差数列的通项公式及前n项和公式求解.
解答 解:∵等差数列{an}的前n项和为Sn,且a4=16,a10=8,
∴S13=$\frac{13}{2}({a}_{1}+{a}_{13})$=$\frac{13}{2}({a}_{4}+{a}_{10})$=$\frac{13}{2}×(16+8)$=156.
故答案为:156.
点评 本题考查等差数列的前13项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
13.随机变量X的分布列如下,则m=( )
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | m | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
8.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程是y=$\frac{4}{3}$x,则该双曲线的离心率是( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
5.P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上的一点,F1,F2是焦点,PF1与渐近线平行,∠F1PF2=90°,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
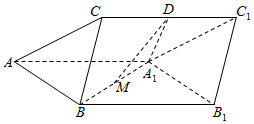 如图,三棱柱ABC-A1B1C1中,D,M分别为CC1和A1B的中点,A1D⊥CC1,侧面ABB1A1为菱形且∠BAA1=60°,AA1=A1D=2,BC=1,
如图,三棱柱ABC-A1B1C1中,D,M分别为CC1和A1B的中点,A1D⊥CC1,侧面ABB1A1为菱形且∠BAA1=60°,AA1=A1D=2,BC=1,