题目内容
5.P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上的一点,F1,F2是焦点,PF1与渐近线平行,∠F1PF2=90°,则双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 求出双曲线的渐近线方程,根据直线平行的关系结合直角三角形的边角关系,求出a,c的关系即可得到结论.
解答 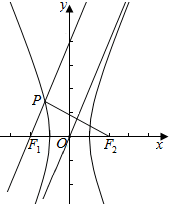 解:双曲线的一条渐近线方程为y=$\frac{b}{a}$x,
解:双曲线的一条渐近线方程为y=$\frac{b}{a}$x,
则$tanα=\frac{b}{a}$,∴$sinα=\frac{b}{c}$,$cosα=\frac{a}{c}$,
∴$sinβ=cosα=\frac{a}{c}$,$\frac{{|{P{F_2}}|-|{P{F_1}}|}}{sinα-sinβ}=\frac{{|{{F_1}{F_2}}|}}{{sin∠{F_1}P{F_2}}}$,
∴$\frac{2a}{{\frac{b}{c}-\frac{a}{c}}}=\frac{2c}{1}$,
∴2a=b,c2-a2=4a2,即c2=5a2,c=$\sqrt{5}$a,
∴$e=\sqrt{5}$,
故选D.
点评 本题考查双曲线的离心率的求法,根据直线平行和直角三角形的边角关系建立方程是解决本题的关键.考查运算能力.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
10.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线互相垂直,那么此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
17.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的斜率为2,过右焦点F作x轴的垂线交双曲线与A,B两点,△OAB(O为坐标原点)的面积为4$\sqrt{5}$,则F到一条渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
14.已知倾斜角为$\frac{π}{3}$的直线与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)相交于A,B两点,M(4,2)是弦AB的中点,则双曲线C的离心率是( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}+1}{2}$ |
15.已知F1、F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过点F1的直线与双曲线C的左、右两支分别交于P、Q两点,|F1P|、|F2P|、|F1Q|成等差数列,且∠F1PF2=120°,则双曲线C的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
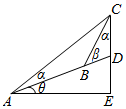 在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为α,向山顶前进a米到达点B,从B点测得斜度为β,设建筑物的高为h米,山坡对于地平面的倾斜角为θ,则cosθ=$\frac{asinαsinβ}{hsin(β-α)}$.
在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为α,向山顶前进a米到达点B,从B点测得斜度为β,设建筑物的高为h米,山坡对于地平面的倾斜角为θ,则cosθ=$\frac{asinαsinβ}{hsin(β-α)}$.