题目内容
已知数列{an}中，an＝1＋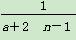
(n∈N*，a∈R，且a≠0)．
(1)若a＝－7，求数列{an}中的最大项和最小项的值；
(2)若对任意的n∈N*，都有an≤a6成立，求a的取值范围．
解 (1)∵an＝1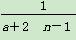＋(n∈N*，a∈R，且a≠0)．
又∵a＝－7，∴an＝1＋
.
结合函数f(x)＝1＋
的单调性，可知1>a1>a2>a3>a4，a5>a6>a7>…>an>1(n∈N*)．
∴数列{an}中的最大项为a5＝2，最小项为a4＝0.
(2)
∵对任意的n∈N*，都有an≤a6成立，
结合函数f(x)＝1＋
的单调性，
，∴－10<a<－8.
练习册系列答案
相关题目
；
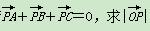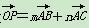m，n∈R)，用x，y表示m－n，并求m－n的最大值．
，则a5＝( )
B.
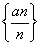是递增数列；