题目内容
数列{an}满足a1=
,an+1=1-
,则a2014等于( )
| 1 |
| 2 |
| 1 |
| an |
A、
| ||
| B、-1 | ||
| C、2 | ||
| D、3 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据数列的递推关系得到数列的规律,即可得到结论.
解答:
解:∵a1=
,an+1=1-
,
∴a2=1-
=1-2=-1,
a3=1-
=1+1=2,
a4=1-
=
,
…
∴{an}的取值具备周期性,周期性3,
则a2014=a671×3+1=a1=
,
故选:A.
| 1 |
| 2 |
| 1 |
| an |
∴a2=1-
| 1 | ||
|
a3=1-
| 1 |
| -1 |
a4=1-
| 1 |
| 2 |
| 1 |
| 2 |
…
∴{an}的取值具备周期性,周期性3,
则a2014=a671×3+1=a1=
| 1 |
| 2 |
故选:A.
点评:本题主要考查递推数列的应用,根据递推数列得到数列{an}的取值具备周期性是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等差数列{an}的前n项和为sn,s6=114,s10=150,则使得sn取最大值时n的值为( )
| A、11或12 | B、12 |
| C、13 | D、12或13 |
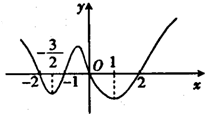 已知函数f(x)的导函数f′(x),函数y=xf′(x)的图象如图所示,则函数f(x)的增区间是( )
已知函数f(x)的导函数f′(x),函数y=xf′(x)的图象如图所示,则函数f(x)的增区间是( )| A、(-2,-1) | ||
B、(-
| ||
| C、(1,+∞) | ||
| D、(0,2) |
复数z=i(-3-2i)(i为虚数单位)在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
复数
的值是( )
| 2-i |
| 3-4i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知在△ABC中,点D在BC边上,且
=2
=r
+s
,则2r+s的值是( )
| CD |
| DB |
| AB |
| AC |
| A、0 | ||
B、
| ||
| C、2 | ||
D、
|
已知a>0,b>0,利用函数f(x)=3x+kx(k>0)的单调性,下列结论正确的是( )
| A、若3a+2a=3b+3b,则a>b |
| B、若3a+2a=3b+3b,则a<b |
| C、若2a-2a=2b-3b,则a>b |
| D、若2a-2a=2b-3b,则a<b |
已知x,y∈R,若lne-1i+2=y+xi,则x3+y=( )
| A、9 | B、3 | C、1 | D、2 |