题目内容
1.已知函数y=lg(ax2+x+1)(1)若函数定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围.
分析 (1)转化为ax2+x+1>0恒成立,利用二次函数性质求解,
(2)理解函数的值域为R,则ax2+x+1能取遍所有的正数,根二次函数性质得出a>0且△=1-4a≥0.
解答 解:(1)∵函数的定义域为R,
∴ax2+x+1>0恒成立.
当a=0时,显然不成立.
当a≠0时,应有a>0且△=-4a<0,
解得 a>$\frac{1}{4}$.
故a的取值范围为:a$>\frac{1}{4}$,
(2)若函数的值域为R,则ax2+x+1能取遍所有的正数,图象不能在x轴上方
∴$\left\{\begin{array}{l}{a>0}\\{△=1-4a≥0}\end{array}\right.$或a=0
解得:0≤a$≤\frac{1}{4}$,
故a的取值范围为[0,$\frac{1}{4}$]
点评 本题考查了对数函数的性质,二次函数的性质,不等式的运用,属于综合题目,关键转化为不等式,理解好二次函数的性质.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
11.平面α与平面β平行的条件可以是( )
| A. | α内有无穷多条直线都与β平行 | B. | 直线a∥α,a∥β且a?α,a?β | ||
| C. | 直线a?α,b?β且a∥β,b∥α | D. | α内的任意直线都与β平行 |
16.函数$f(x)=|lg({x-\frac{1}{2}})|-cosx$的零点的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.执行如图所示的程序框图,输出S的值是( )


| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
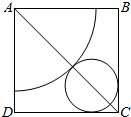 在边长为a的正方形ABCD中,剪下一个扇形和一个圆,如图所示,分别作为圆锥的侧面和底面,求所围成的圆锥的体积.
在边长为a的正方形ABCD中,剪下一个扇形和一个圆,如图所示,分别作为圆锥的侧面和底面,求所围成的圆锥的体积.