题目内容
已知函数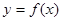 的定义域为
的定义域为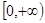 ,且对于任意
,且对于任意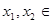
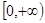 ,存在正实数L,使得
,存在正实数L,使得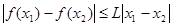 均成立。
均成立。
(1)若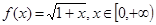 ,求正实数L的取值范围;
,求正实数L的取值范围;
(2)当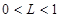 时,正项数列{
时,正项数列{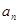 }满足
}满足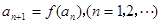
①求证: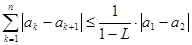 ;
;
②如果令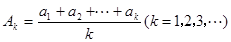 ,求证:
,求证: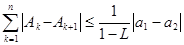 .
.
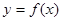 的定义域为
的定义域为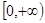 ,且对于任意
,且对于任意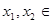
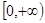 ,存在正实数L,使得
,存在正实数L,使得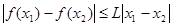 均成立。
均成立。(1)若
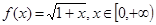 ,求正实数L的取值范围;
,求正实数L的取值范围;(2)当
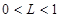 时,正项数列{
时,正项数列{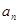 }满足
}满足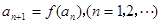
①求证:
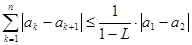 ;
;②如果令
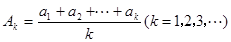 ,求证:
,求证: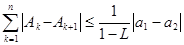 .
.(1) (2)证明如下
(2)证明如下
 (2)证明如下
(2)证明如下试题分析:解:(1)由已知可得,对任意的
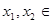
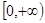 ,均有
,均有 ,
,又由
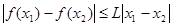 恒成立,即
恒成立,即 恒成立.
恒成立.当
 时,由上可得
时,由上可得 .因为
.因为 ,故
,故 ,故
,故 ;
;当
 时,
时,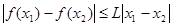 恒成立。
恒成立。 的取值范围是
的取值范围是 .
.(2)①因为
 ,故当
,故当 时,
时,

 ,所以
,所以
 .因为
.因为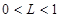 ,所以
,所以 (当
(当 时,不等式也成立).
时,不等式也成立).②因为
 ,所以
,所以


 .所以
.所以


 .
.点评:本题难度较大。关于不等式的证明,常用到的方法较多,像放缩法、裂变法、绝对值性质法和基本不等式法等。

练习册系列答案
相关题目
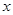 是
是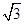 的一个近似值,令
的一个近似值,令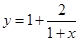 .
.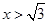 ,求证:
,求证: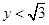 ;
; 与
与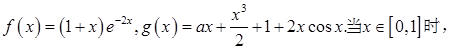

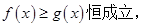
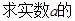 取值范围.
取值范围.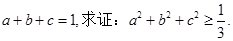
 , 求证:
, 求证: .
. ,求证:
,求证: .
.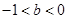 ,
, ,那么下列不等式成立的是( )
,那么下列不等式成立的是( )



 ,
, 满足
满足 ,求证:
,求证:

