题目内容
19.过抛物线y2=16x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|=( )| A. | 8 | B. | 10 | C. | 14 | D. | 16 |
分析 抛物线 y2=16x的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点,故|AB|=x1+x2+8,由此易得弦长值.
解答 解:由题意,p=8,故抛物线的准线方程是x=-4,
∵抛物线 y2=16x 的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点
∴|AB|=x1+x2+8,
又x1+x2=6
∴∴|AB|=x1+x2+8=14
故选C.
点评 本题考查抛物线的简单性质,解题的关键是理解到焦点的距离与到准线的距离相等,由此关系将求弦长的问题转化为求点到线的距离问题,大大降低了解题难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.集合M={(x,y)|x2+y2=1},N={(x,y)|x2+y2=4},集合M与N的关系是( )
| A. | M=N | B. | M⊆N | ||
| C. | N⊆M | D. | M,N不存在包含关系 |
14.抛物线x=2ay2的准线方程是x=2,则a的值是( )
| A. | $\frac{1}{16}$ | B. | $-\frac{1}{16}$ | C. | -4 | D. | 4 |
4.已知m,n是两条不同直线,α,β是两个不同的平面,且n?β,则下列叙述正确的是( )
| A. | 若m∥n,m?α,则α∥β | B. | 若α∥β,m?α,则m∥n | C. | 若α∥β,m⊥n,则m⊥α | D. | 若m∥n,m⊥α,则α⊥β |
11.已知抛物线x=4y2上一点P(m,1),焦点为F.则|PF|=( )
| A. | m+1 | B. | 2 | C. | $\frac{63}{16}$ | D. | $\frac{65}{16}$ |
9.当用反证法证明“已知x>y,证明:x3>y3”时,假设的内容应是( )
| A. | x3≤y3 | B. | x3<y3 | C. | x3>y3 | D. | x3≥y3 |
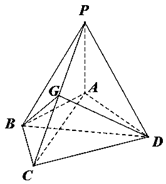 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,∠ABC=120°,G为线段PC上的点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,∠ABC=120°,G为线段PC上的点.