题目内容
10.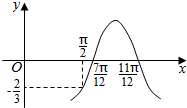 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )| A. | 1 | B. | x | C. | 0 | D. | $\frac{2}{3}$$\sqrt{2}$ |
分析 首先,根据图象得到函数周期,利用周期公式可求ω,由题意可得点($\frac{\frac{11π}{12}+\frac{7π}{12}}{2}$,A)在函数图象上,可得φ=2kπ-$\frac{7π}{4}$,k∈Z,结合范围0<φ<π,即可求φ,由f($\frac{π}{2}$)=-$\frac{2}{3}$可求A的值.
解答 解:根据图象得到:A=2,
∴T=2($\frac{11π}{12}$-$\frac{7π}{12}$)=$\frac{2π}{3}$=$\frac{2π}{ω}$,
∴ω=3,
∴f(x)=Asin(3x+φ),
∵由题意可得,点($\frac{\frac{11π}{12}+\frac{7π}{12}}{2}$,A)在函数图象上,可得:Asin($\frac{\frac{11π}{12}+\frac{7π}{12}}{2}$×3+φ)=A,即:sin($\frac{\frac{11π}{12}+\frac{7π}{12}}{2}$×3+φ)=1,
∴解得:φ=2kπ-$\frac{7π}{4}$,k∈Z,
∵0<φ<π,
∴φ=$\frac{π}{4}$,
又∵f($\frac{π}{2}$)=Asin(3×$\frac{π}{2}$+$\frac{π}{4}$)=A×(-$\frac{\sqrt{2}}{2}$)=-$\frac{2}{3}$,
∴解得:A=$\frac{2\sqrt{2}}{3}$.
故选:D.
点评 本题重点考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的图象与性质及其运用,由点($\frac{\frac{11π}{12}+\frac{7π}{12}}{2}$,A)在函数图象上求φ是解题的关键,属于中档题.

| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“若一个数是负数,则它的平方是正数”的逆命题是“若一个数的平方不是正数,则它不是负数” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1<0” |
| A. | 4 | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |
| A. | A=R,B={x|x是正实数},f:A中的数的绝对值 | |
| B. | A={0,1},B={-1,0,1},f:A中的数的开方 | |
| C. | A=Z,B=Q,f:A中的数的倒数 | |
| D. | A={-1,0,1},B={-1,0,1},f:A中的数的平方 |
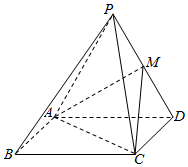 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3.