题目内容
1．下列有关命题的说法正确的是（ ）| A． | 命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” | |
| B． | 命题“若一个数是负数，则它的平方是正数”的逆命题是“若一个数的平方不是正数，则它不是负数” | |
| C． | 命题“若x=y，则sinx=siny”的逆否命题为真命题 | |
| D． | 命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R均有x2+x+1＜0” |
分析 写出命题的否命题判断A；写出命题的逆命题判断B；由互为逆否命题的两个命题共真假判断C；直接写出特称命题的否定判断D．
解答 解：命题“若x2=1，则x=1”的否命题为：“若x2≠1，则x≠1”，故A错误；
命题“若一个数是负数，则它的平方是正数”的逆命题是“若一个数的平方是正数，则这个数是负数”，故B错误；
命题“若x=y，则sinx=siny”为真命题，故其逆否命题为真命题，C正确；
命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R均有x2+x+1≥0”，故D错误．
故选：C．
点评 本题考查命题的真假判断与应用，考查了命题的逆命题、否命题以及逆否命题的真假判断，考查特称命题的否定，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．“?x∈R，ex-2＞m”是“m2＞2”成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
13．已知函数f（x-1）的定义域是[-1，3]，则f（x）=f（2x）+lg（1-x）的定义域为（ ）
| A． | [-1，1] | B． | [-1，1） | C． | [-4，1） | D． | [-4，1] |
10．
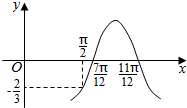已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，f（$\frac{7π}{12}$）=0，f（$\frac{11π}{12}$）=0，则A=（ ）
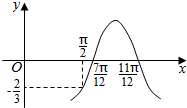已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，f（$\frac{7π}{12}$）=0，f（$\frac{11π}{12}$）=0，则A=（ ）| A． | 1 | B． | x | C． | 0 | D． | $\frac{2}{3}$$\sqrt{2}$ |