题目内容
已知函数f(x)=lnx-
ax2-2x.
(1)若a=3,求f(x)的增区间;
(2)若a<0,且函数f(x)存在单调递减区间,求a的取值范围;
(3)若a=-
且关于x的方程f(x)=-
x+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.
| 1 |
| 2 |
(1)若a=3,求f(x)的增区间;
(2)若a<0,且函数f(x)存在单调递减区间,求a的取值范围;
(3)若a=-
| 1 |
| 2 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)在定义域内解不等式f′(x)>0即可;
(2)由函数f(x)存在单调递减区间,知f′(x)<0在(0,+∞)上有解,分离参数化为函数最值即可;
(3)f(x)=-
x+b化为b=lnx+
x2-
x,令g(x)=lnx+
x2-
x(1≤x≤4),利用导数求得g(x)的最值,借助图象可得结果;
(2)由函数f(x)存在单调递减区间,知f′(x)<0在(0,+∞)上有解,分离参数化为函数最值即可;
(3)f(x)=-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
解答:
解:(1)f(x)的定义域是(0,+∞),
a=3时,f′(x)=
-3x-2=
,
令f′(x)>0,得0<x<
,
∴函数f(x)的增区间是(0,
].
(2)f′(x)=
-ax-2,
由函数f(x)存在单调递减区间,知f′(x)<0在(0,+∞)上有解,
∴
-ax-2<0,即a>
-
,
而
-
=(
-1)2-1≥-1,
∴a>-1,又a<0,
∴-1<a<0.
(3)a=-
时,f(x)=lnx+
x2-2x,则f(x)=-
x+b即为b=lnx+
x2-
x,
令g(x)=lnx+
x2-
x(1≤x≤4),则g′(x)=
+
x-
=
,
当1<x<2时,g′(x)<0,g(x)递减;当2<x<4时,g′(x)>0,g(x)递增.
∴g(x)min=g(2)=ln2-2,
又g(1)=-
,g(4)=ln4-2,g(1)<g(4),
∴ln2-2<b≤-
,即实数b的取值范围是ln2-2<b≤-
.
a=3时,f′(x)=
| 1 |
| x |
| -(3x-1)(x+1) |
| x |
令f′(x)>0,得0<x<
| 1 |
| 3 |
∴函数f(x)的增区间是(0,
| 1 |
| 3 |
(2)f′(x)=
| 1 |
| x |
由函数f(x)存在单调递减区间,知f′(x)<0在(0,+∞)上有解,
∴
| 1 |
| x |
| 1 |
| x2 |
| 2 |
| x |
而
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| x |
∴a>-1,又a<0,
∴-1<a<0.
(3)a=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
令g(x)=lnx+
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| (x-1)(x-2) |
| 2x |
当1<x<2时,g′(x)<0,g(x)递减;当2<x<4时,g′(x)>0,g(x)递增.
∴g(x)min=g(2)=ln2-2,
又g(1)=-
| 5 |
| 4 |
∴ln2-2<b≤-
| 5 |
| 4 |
| 5 |
| 4 |
点评:该题考查利用导数研究函数的单调性、最值,考查方程的根,考查函数与方程思想、数形结合思想,属中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
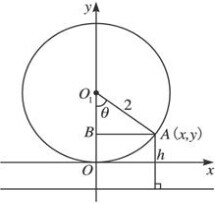 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.
如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.