题目内容
7.已知数列{an}满足a1=1,${a_{n+1}}=\left\{{\begin{array}{l}{2{a_n},n为正奇数}\\{{a_n}+1,n为正偶数}\end{array}}\right.$,则254是该数列的( )| A. | 第14项 | B. | 第12项 | C. | 第10项 | D. | 第8项 |
分析 当n为奇数时,可推出an+1=2(an-2+1),从而可得an=${2}^{\frac{n+1}{2}}$-1,从而先解254的前一项,即254=2(${2}^{\frac{n+1}{2}}$-1),从而解得.
解答 解:当n为奇数时,
an=an-1+1=2an-2+1,
故an+1=2(an-2+1),
故an+1=(1+1)•${2}^{\frac{n-1}{2}}$=${2}^{\frac{n+1}{2}}$,
故an=${2}^{\frac{n+1}{2}}$-1,
故254不是奇数项,
故254=2(${2}^{\frac{n+1}{2}}$-1),
故n=13,
故254是该数列的第14项,
故选:A.
点评 本题考查了数列的递推关系的应用及构造法的应用.

练习册系列答案
相关题目
15.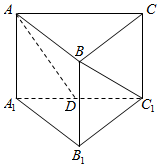 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
2.e为自然对数的底数,定义函数shx=$\frac{{e}^{x}-{e}^{-x}}{2}$,chx=$\frac{{e}^{x}+{e}^{-x}}{2}$,若已知函数f(x)为奇函数,且满足f(1)=ch1,当x>0时,f(x)+xf′(x)>shx,则f(x)<$\frac{chx}{x}$的解集为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
19.下列程序执行后输出的结果是( )


| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
16.定义在R上的偶函数满足f(x+2)=f(x),且在[0,1]上单调递增,设a=f(3),$b=f(\sqrt{2})$,c=f(2),则a,b,c的大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
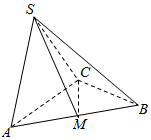 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.