题目内容
2.设{an}是等比数列,公比为q(q>0且q≠1),4a1,3a2,2a3成等差数列,且它的前4项和为S4=15.(1)求{an}通项公式;
(2)令bn=an+2n(n=1,2,3…),求{bn}的前n项和.
分析 (1)通过4a1,3a2,2a3成等差数列,利用首项、公比表示出前三项计算可知公比为2,利用前四项和计算可知首项,进而可得通项公式;
(2)通过(1)可知bn=2n-1+2n,进而利用分组法求和即可.
解答 解:(1)∵4a1,3a2,2a3成等差数列,
∴2×3a2=4a1+2a3,
又∵数列{an}是等比数列,
∴6a1q=4a1+2${a}_{1}{q}^{2}$,即q2-3q+2=0,
解得:q=2或q=1(舍),
又∵S4=15,
∴$\frac{{a}_{1}(1-{2}^{4})}{1-2}$=15,即a1=1,
∴数列{an}是首项为1、公比为2的等比数列,
∴数列{an}通项公式an=2n-1;
(2)由(1)可知bn=2n-1+2n(n=1,2,3…),
∴数列{bn}的前n项和为$\frac{1-{2}^{n}}{1-2}$+2•$\frac{n(n+1)}{2}$=2n+n2+n-1.
点评 本题考查数列的通项及前n项和,考查分组法求和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
17.tan70°cos10°+$\sqrt{3}$sin10°tan70°-2sin50°=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
11.等差数列{an}中,a3=2,a6=5,则数列{${2}^{{a}_{n}}$}的前5项和等于( )
| A. | 15 | B. | 31 | C. | 63 | D. | 127 |
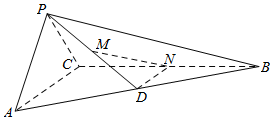 在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.
在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.