题目内容
13.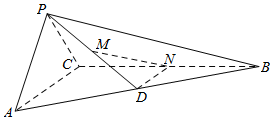 在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.
在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.(Ⅰ)当N为BC的中点时,证明:DN∥平面PAC;
(Ⅱ)求证:PA⊥平面PBC;
(Ⅲ)是否存在点N使得MN∥平面PAC?若存在,求出$\frac{CN}{CB}$的值,若不存在,说明理由.
分析 (Ⅰ)由三角形中位线定理得DN∥AC,由此能证明DN∥平面PAC.
(Ⅱ)由已知得BC⊥平面PAC,PA⊥BC,PA⊥PC,由此能证明PA⊥平面PBC.
(Ⅲ)取AD中点E,连结ME、NE,推导出平面MEN∥平面PAC,从而得到存在点N,当$\frac{CN}{CB}=\frac{1}{4}$时,MN∥平面PAC.
解答 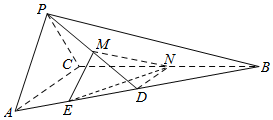 证明:(Ⅰ)∵D为AB的中点,N为BC的中点,
证明:(Ⅰ)∵D为AB的中点,N为BC的中点,
∴DN∥AC,
∵DN?平面PAC,AC?平面PAC,
∴DN∥平面PAC.
(Ⅱ)∵平面PAC⊥平面ABC,AC⊥BC,
∴BC⊥平面PAC,
∵PA?平面PAC,∴PA⊥BC,
∵PA⊥PC,PC∩BC=C,
∴PA⊥平面PBC.
解:(Ⅲ)存在点N,当$\frac{CN}{CB}=\frac{1}{4}$时,MN∥平面PAC.
理由如下:
取AD中点E,连结ME、NE,
∵M为PD中点,∴ME∥PA,
∵D为AB中点,E为AD中点,∴$\frac{AE}{AB}=\frac{1}{4}$,
又∵$\frac{CN}{CB}$=$\frac{1}{4}$,∴EN∥AC,
∵ME∩NE=E,ME、EN?平面MEN,PA、AC?平面PAC,
∴平面MEN∥平面PAC,
∵MN?平面MEN,∴MN∥平面PAC.
∴存在点N,当$\frac{CN}{CB}=\frac{1}{4}$时,MN∥平面PAC.
点评 本题考查线面平行的证明,考查线面垂直的证明,考查满足线面平行的点是否存在的判断与求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.已知函数$f(x)=\left\{\begin{array}{l}{{2}^{x-1}-2,x≤1}\\{-lo{g}_{2}(x+1),x>1}\end{array}\right.$且f(a)≥-2,则实数a的取值范围是( )
| A. | (-∞,1] | B. | [3,+∞) | C. | (-∞,3] | D. | [1,3] |
18.若a>b,则下列不等式成立的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | a3>b3 | D. | a2>b2 |