题目内容
如果集合A={x|ax2+2x+1=0}中只有一个元素，则a的值是（ ）
| A、0 | B、0 或1 |
| C、1 | D、不能确定 |
考点：元素与集合关系的判断
专题：分类讨论
分析：从集合A只有一个元素入手，分为a=0与a≠0两种情况进行讨论，即可得到正确答案．
解答：
∵A={x|ax2+2x+1=0}中只有一个元素，
当a=0时，A={x|2x+1=0}，即A={-
}．
当a≠0时，需满足△=b2-4ac=0，即22-4×a×1=0，a=1．
∴当a=0或a=1时满足A中只有一个元素．
故答案为：B
当a=0时，A={x|2x+1=0}，即A={-
| 1 |
| 2 |
当a≠0时，需满足△=b2-4ac=0，即22-4×a×1=0，a=1．
∴当a=0或a=1时满足A中只有一个元素．
故答案为：B
点评：本题考查了元素与集合的关系，需分情况对问题进行讨论，为基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
设A={y|y=log2x，x＞1}，B={-2，-1，1，2}则下列结论正确的是（ ）
| A、A∩B={-2，-1} |
| B、（∁RA）∪B=（-∞，0） |
| C、A∪B=（0，+∞） |
| D、（∁RA）∩B={-2，-1} |
”a＜0”是”函数f（x）=|x（x-2a）|在区间（0，+∞）上单调递增”的（ ）
| A、必要不充分条件 |
| B、充要条件 |
| C、既不充分也不必要条件 |
| D、充分不必要条件 |
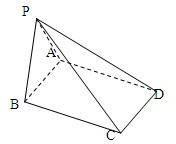如图，四棱锥P-ABCD的底面是AB=2，BC=