题目内容
设函数f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+x-3,则f(x)的零点个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:函数零点的判定定理,函数奇偶性的性质
专题:函数的性质及应用
分析:先由函数f(x)是定义在R上的奇函数确定0是一个零点,再令x>0时的函数f(x)的解析式等于0转化成两个函数,转化为判断两函数交点个数问题,最后根据奇函数的对称性确定答案.
解答:
解:∵函数f(x)是定义域为R的奇函数,
∴f(0)=0,所以0是函数f(x)的一个零点
当x>0时,令f(x)=ex+x-3=0,
则ex=-x+3,
分别画出函数y=ex,和y=-x+3的图象,如图所示,有一个交点,所以函数f(x)有一个零点,
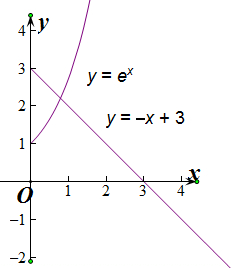
又根据对称性知,当x<0时函数f(x)也有一个零点.
综上所述,f(x)的零点个数为3个,
故选C.
∴f(0)=0,所以0是函数f(x)的一个零点
当x>0时,令f(x)=ex+x-3=0,
则ex=-x+3,
分别画出函数y=ex,和y=-x+3的图象,如图所示,有一个交点,所以函数f(x)有一个零点,
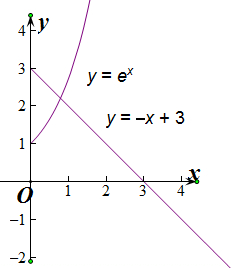
又根据对称性知,当x<0时函数f(x)也有一个零点.
综上所述,f(x)的零点个数为3个,
故选C.
点评:本题是个基础题,函数的奇偶性是函数最重要的性质之一,同时函数的奇偶性往往会和其他函数的性质结合应用,此题就与函数的零点结合,符合高考题的特点.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
设函数f(x)=loga(x-a+2)在区间(1,+∞)上恒为正值,则实数a的取值范围是( )
| A、(1,2] | ||
| B、(1,2) | ||
| C、(0,1)∪(1,2) | ||
D、(1,
|
下列算式正确的是( )
| A、log2(3π)=log23+log2π | ||||||
B、
| ||||||
C、
| ||||||
D、5
|