题目内容
2.已知若0$<α<\frac{π}{2}$,-$\frac{π}{2}$<β<0,cos($\frac{π}{4}$+α)=$\frac{1}{3}$,cos($\frac{π}{4}$-$\frac{β}{2}$)=$\frac{\sqrt{3}}{3}$求(1)求cosα的值;
(2)求$cos({α+\frac{β}{2}})$的值.
分析 由条件利用同角三角函数的基本关系,两角和差的余弦公式求得cosα、$cos({α+\frac{β}{2}})$的值.
解答 解:(1)∵$0<α<\frac{π}{2}$,∴$\frac{π}{4}<\frac{π}{4}+α<\frac{3π}{4}$.
∵$cos(\frac{π}{4}+α)=\frac{1}{3}$,∴$sin(\frac{π}{4}+α)=\frac{{2\sqrt{2}}}{3}$,
∴$cosα=cos(\frac{π}{4}+α-\frac{π}{4})=cos(\frac{π}{4}+α)cos\frac{π}{4}+sin(\frac{π}{4}+α)sin\frac{π}{4}=\frac{{\sqrt{2}+4}}{6}$.
(2)∵$-\frac{π}{2}<β<0$,∴$\frac{π}{4}<\frac{π}{4}-\frac{β}{2}<\frac{π}{2}$.
∵$cos(\frac{π}{4}-\frac{β}{2})=\frac{{\sqrt{3}}}{3}$,∴$sin(\frac{π}{4}-\frac{β}{2})=\frac{{\sqrt{6}}}{3}$,
∴$cos(α+\frac{β}{2})=cos[(\frac{π}{4}+α)-(\frac{π}{4}-\frac{β}{2})]=cos(\frac{π}{4}+α)cos(\frac{π}{4}-\frac{β}{2})+sin(\frac{π}{4}+α)sin(\frac{π}{4}-\frac{β}{2})=\frac{{5\sqrt{3}}}{9}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的余弦公式的应用,属于基础题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
| A. | (2,2018) | B. | (2,2019) | C. | (3,2018) | D. | (3,2019) |
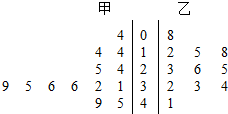 现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.
现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.