题目内容
1.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的中心,右焦点和右顶点分别为O,F,A,右准线与x轴的交点为H,则$\frac{FA}{OH}$的最大值为$\frac{1}{4}$.分析 由题意可得:$\frac{FA}{OH}$=$\frac{a-c}{\frac{{a}^{2}}{c}}$=-e2+e,利用二次函数的单调性即可得出.
解答 解:∵e∈(0,1),
由题意可得:$\frac{FA}{OH}$=$\frac{a-c}{\frac{{a}^{2}}{c}}$=$\frac{ac-{c}^{2}}{{a}^{2}}$=-e2+e=-$(e-\frac{1}{2})^{2}$+$\frac{1}{4}$∈$(0,\frac{1}{4}]$,
故$\frac{FA}{OH}$的最大值为$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查了椭圆的定义标准方程及其性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知数列{an}是公差不为0的等差数列,Sn为其前n项和,若S2=3S1且S1+9,S2+9,S3+9成等比数列,则2016是数列{an}的第( )项.
| A. | 671 | B. | 672 | C. | 673 | D. | 674 |
12.设a=${log_{\frac{1}{2}}}$3,b=${(\frac{1}{3})^{0.2}}$,c=${(\frac{1}{2})^{-\frac{1}{2}}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |
16.已知a=log23,b=(log23)2,c=(${\frac{1}{4}}$)-1.2,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
11.若a≥0,b≥0,且当$\left\{\begin{array}{l}{|x|≤1}\\{|y|≤1}\end{array}\right.$时,恒有2ax+by≤1,则点P(a+b,a-b)所形成的平面区域的面积是( )
| A. | $\frac{π}{2}$ | B. | 2π | C. | 1 | D. | $\frac{1}{2}$ |
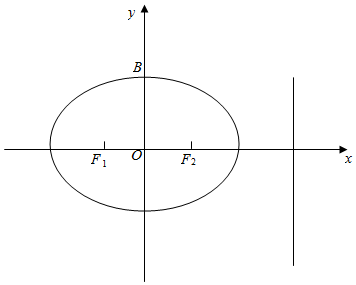 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.