题目内容
11.已知数列{an}是公差不为0的等差数列,Sn为其前n项和,若S2=3S1且S1+9,S2+9,S3+9成等比数列,则2016是数列{an}的第( )项.| A. | 671 | B. | 672 | C. | 673 | D. | 674 |
分析 设数列{an}的公差为d(d≠0),运用等差数列的通项公式,可得首项和公差相等,再由等比数列的中项的性质,解方程可得d=3,求得数列的通项公式,可令an=2016,解方程即可得到所求n.
解答 解:设数列{an}的公差为d(d≠0),
即有S1=a1,S2=2a1+d,S3=3a1+3d,
由S2=3S1,可得a1=d,
由S1+9,S2+9,S3+9成等比数列,可得
(S1+9)(S3+9)=(S2+9)2,
即为(a1+9)(3a1+3d+9)=(2a1+d+9)2,
即有(d+9)(6d+9)=(3d+9)2,
解得d=3(d=0舍去).
即有an=a1+(n-1)d=nd=3n,
由2016=3n,可得n=672.
故选:B.
点评 本题考查等差数列的通项公式的运用,以及等比数列的中项的性质,考查化简整理的运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.若函数f(x)=2x+b-1(b∈R)的图象不经过第二象限,则有( )
| A. | b≥1 | B. | b≤1 | C. | b≥0 | D. | b≤0 |
3.$\frac{7}{16}$-$\frac{7}{8}$sin215°的值为( )
| A. | $\frac{7}{32}$ | B. | $\frac{7\sqrt{3}}{32}$ | C. | $\frac{7}{16}$ | D. | $\frac{7\sqrt{3}}{16}$ |
20.函数y=2lnx-$\frac{1}{{x}^{2}}$的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
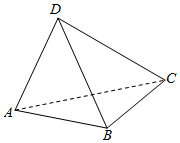 如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.
如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2. 如图是甲、乙两位同学在5次数学测试中得分的茎叶图,则成绩较稳定(方差较小)的那一位同学的方差为2.
如图是甲、乙两位同学在5次数学测试中得分的茎叶图,则成绩较稳定(方差较小)的那一位同学的方差为2.