题目内容
9.甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,记录如下:| 甲 | 88 | 89 | 92 | 90 | 91 |
| 乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
分析 (Ⅰ)作出茎叶图即可;(Ⅱ)分别计算平均数和方差,通过比较平均数和方差的大小,即可得到结论.
解答 解:(Ⅰ)作出茎叶图如下: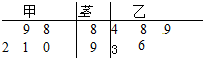 ,
,
(Ⅱ)派甲参赛比较合适,
理由如下${\overline x_{_甲}}=\frac{1}{5}(88+89+90+91+92)=90$,
$\overline{x_乙}=\frac{1}{5}(84+88+96+89+93)=90$,
${{S}_{甲}}^{2}$=$\frac{1}{5}$[(88-90)2+(89-90)2+(90-90)2+(91-90)2+(92-90)2]=2,
${{S}_{乙}}^{2}$=$\frac{1}{5}$[(84-90)2+(88-90)2+(89-90)2+(93-90)2+(96-90)2]=17.2,
∵$\overline{x_甲}=\overline{x_乙}$,${{S}_{甲}}^{2}$<${{S}_{乙}}^{2}$,
∴从质量的稳定性角度考虑,采购甲药厂的产品比较合适.
点评 本题主要考查统计的应用,要求熟练平均数和方差的公式和计算.

练习册系列答案
相关题目
14.已知等比数列{an}中,a1=4,a5a7=4a82,则a3=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 1 |
1.若复数z=a+bi(a,b∈R,i为虚数单位)满足z2=-1,则b=( )
| A. | 1 | B. | ±1 | C. | i | D. | ±i |
18.已知${log_{\frac{1}{2}}}$(x+y+4)<${log_{\frac{1}{2}}}$(3x+y-2),若x-y<λ+$\frac{9}{λ}$恒成立,则λ的取值范围是( )
| A. | (-∞,1)∪(9,+∞) | B. | (1,9) | C. | (0,1)∪(9,+∞) | D. | (0,1]∪[9,+∞) |
19.使不等式2x-4>0成立的一个充分不必要条件是( )
| A. | x>2 | B. | x>3 | C. | x>1 | D. | x∈{1,2} |
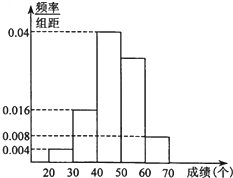 体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.
体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.