题目内容
20.已知A类产品共两件A1,A2,B类产品共三件B1,B2,B3,混放在一起,现需要通过检测将其区分开来,每次随机检测一件产品,检测后不放回,直到检测出2件A类产品或者检测出3件B类产品时,检测结束.(Ⅰ)求第一次检测出B类产品,第二次检测出A类产品的概率;
(Ⅱ)已知每检测一件产品需要费用50元,设X表示直到检测出2件A类产品或者检测出3件B类产品时所需要的检测费用(单位:元),求X的分布列和均值.
分析 (Ⅰ)记“第一次检测出B类产品,第二次检测出A类产品”的事件为C事件,由此利用等可能事件概率计算公式能求出第一次检测出B类产品,第二次检测出A类产品的概率.
(Ⅱ)X的可能取值为100、150、200,分别求出相应的概率,由此能求出X的分布列的数学期望.
解答 解:(Ⅰ)记“第一次检测出B类产品,第二次检测出A类产品”的事件为C事件,
依题意有$P(C)=\frac{A_3^1•A_2^1}{A_5^2}=\frac{3}{10}$.…(4分)
(Ⅱ)X的可能取值为100、150、200,
$P(X=100)=\frac{A_2^2}{A_5^2}=\frac{1}{10}$,
$P(X=150)=\frac{A_3^3+C_3^1•C_2^1•A_2^2}{A_5^3}=\frac{3}{10}$,
$P(X=200)=1-\frac{1}{10}-\frac{3}{10}=\frac{6}{10}$,…(8分)
故X的分布列为
| X | 100 | 150 | 200 |
P | $\frac{1}{10}$ | $\frac{3}{10}$ | $\frac{6}{10}$ |
$E(X)=100×\frac{1}{10}+150×\frac{3}{10}+200×\frac{6}{10}=175(元)$.…(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
11.在等比数列{an}中,若a1,a2,…,a8都是正数,且公比q≠1,则( )
| A. | a1+a8>a4+a5 | B. | a1+a8<a4+a5 | ||
| C. | a1+a8=a4+a5 | D. | a1+a8与a4+a5的大小关系不定 |
8.若复数z满足z(1+i)=2-2i(i为虚数单位),则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
9.甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,记录如下:
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
| 甲 | 88 | 89 | 92 | 90 | 91 |
| 乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
10.sin330°的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
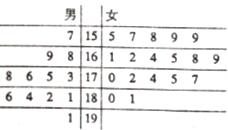 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm): 如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.
如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E. 如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.
如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.