题目内容
已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: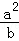 +
+ +
+ ≥1.
≥1.
(1) ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)首先解不等式 ,根据题设列方程解出
,根据题设列方程解出 的值.
的值.
(2)要证 ,只要证:
,只要证: ,即证
,即证
试题解析:【解析】
(1)由f(x+2)≤2得|x﹣4|﹣t≤2,
∴当t+2≥0时,解得﹣t≤x≤t+4,
又∵不等式f(x+2)≤2的解集为[﹣1,5],
∴﹣t=﹣1且t+4=5,∴t=1.
(2)∵a,b,c均为正实数,且a+b+c=1,
∴ +
+ +
+ +(a+b+c)=(
+(a+b+c)=( )+(
)+( +c)+(
+c)+( +a)≥2
+a)≥2 +2
+2 +2
+2 =2(a+b+c)=2
=2(a+b+c)=2
∴ +
+ +
+ ≥1.
≥1.
考点:1、含绝对值的不等式的解法;2、基本不等式.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 是
是 的一条切线,切点为
的一条切线,切点为 ,直线
,直线 ,
, ,
, 都是
都是 的割线,已知
的割线,已知 .
.
 ;
; ,
, .求
.求 的值.
的值.
 (
( ),直线
),直线 过
过 的一个焦点,且垂直于
的一个焦点,且垂直于 轴,直线
轴,直线 与双曲线
与双曲线 交于
交于 ,
, 两点,则
两点,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 <x1x2<1 B.1<x1x2<e
<x1x2<1 B.1<x1x2<e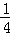 ,乙每次投中的概率为
,乙每次投中的概率为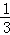 求:
求: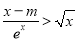 成立,则实数m的取值范围为( )
成立,则实数m的取值范围为( )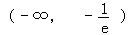
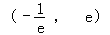

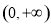
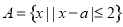 ,
,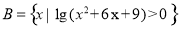 .
.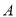 和
和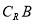 ;
; 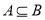 ,求实数
,求实数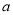 的取值范围.
的取值范围. 是圆
是圆 的切线,
的切线, 是圆
是圆 的割线,若
的割线,若 ,
, ,
, ,则圆
,则圆 .
.