题目内容
在正方形ABCD中,点E在AB边上,且AE∶EB=2∶1,AF⊥DE于G,交BC于F,则△AEG的面积与四边形BEGF的面积比为( )A.1∶2 B.1∶4
C.4∶9 D.2∶3
思路解析:易证△ABF≌△DAE.故知BF=AE.
因AE∶EB=2∶1,故可设AE=2x,EB=x,则AB=3x,BF=2x.
由勾股定理得AF=![]() x.
x.
易证△AEG∽△ABF.
可得S△AEG∶S△ABF=AE2∶AF2=(2x)2∶(![]() x)2=4∶13.
x)2=4∶13.
可得S△AEG∶S四边形BEGF=4∶9.
答案:C

练习册系列答案
相关题目
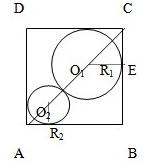 如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆. 在正方形ABCD中,E、F分别为AB、BC的中点,用向量求证:AF⊥DE.
在正方形ABCD中,E、F分别为AB、BC的中点,用向量求证:AF⊥DE. 如图,在正方形ABCD中,M是边BC的中点,N是边CD的中点,设∠MAN=α,那么sinα的值等于
如图,在正方形ABCD中,M是边BC的中点,N是边CD的中点,设∠MAN=α,那么sinα的值等于 (2012•武汉模拟)如图,在正方形ABCD中,点E为CD的中点,点F为BC上靠近点B的一个三等分点,则
(2012•武汉模拟)如图,在正方形ABCD中,点E为CD的中点,点F为BC上靠近点B的一个三等分点,则