题目内容

在正方形ABCD中，E、F分别为AB、BC的中点，用向量求证：AF⊥DE．
分析：可得
AF
=
AB
+
1
2
AD
，
DE
=
1
2
AB
-
AD
，故
AF
•
DE
=
1
2
AB
2-
1
2
AD
2-
3
4
AB
•
AD
=0，可得结论．
解答：解：由题意可得
AF
=
AB
+
BF
=
AB
+
1
2
AD
，
同理
DE
=
AE
-
AD
=
1
2
AB
-
AD
，
故
AF
•
DE
=（
AB
+
1
2
AD
）（
1
2
AB
-
AD
）
=
1
2
AB
2-
1
2
AD
2-
3
4
AB
•
AD

设正方形ABCD的边长为a，
由AB⊥AD可知
AB
•
AD
=0，
故上式=
1
2
a
2-
1
2
a2=0，
故
AF
⊥
DE
，AF⊥DE
点评：本题考查数量积判断两个向量的垂直关系，把向量用同一组向量表示是解决问题的关键，属基础题．
练习册系列答案
相关题目
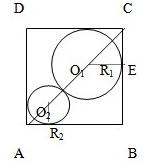精英家教网如图，已知正方形的边长为1，在正方形ABCD中有两个相切的内切圆．
（1）求这两个内切圆的半径之和；
（2）当这两个圆的半径为何值时，两圆面积之和有最小值？当这两个圆的半径为何值时，两圆面积之和有最大值？
如图，在正方形ABCD中，M是边BC的中点，N是边CD的中点，设∠MAN=α，那么sinα的值等于
4
5
4
5
．
在正方形ABCD中，已知它的边长为1，设
AB
=
a
，
BC
=
b
，
AC
=
c
，则|
a
+
b
+
c
|的值为（　　）
（2012•武汉模拟）如图，在正方形ABCD中，点E为CD的中点，点F为BC上靠近点B的一个三等分点，则
EF
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网