题目内容
直线a∥b，a与平面α相交，判定b与平面α的位置关系，并证明你的结论．
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：判定b与平面α的位置关系是b∩α=Q，可用反证法给出证明：如图所示，由于a∥b，可以经过直线a，b确定一个平面β．由于a∩α=P，可得α∩β=l．可得b与直线l必然相交，否则b∥l，得出矛盾．
解答：
解：判定b与平面α的位置关系是b∩α=Q，下面给出证明：
如图所示，
∵a∥b，
∴可以经过直线a，b确定一个平面β．
∵a∩α=P，
∴α∩β=l．
则b与直线l必然相交，否则b∥l，
则a∥l，与a∩l=P相矛盾．
因此b∩l=Q，
∴b∩α=Q．
如图所示，
∵a∥b，∴可以经过直线a，b确定一个平面β．
∵a∩α=P，
∴α∩β=l．
则b与直线l必然相交，否则b∥l，
则a∥l，与a∩l=P相矛盾．
因此b∩l=Q，
∴b∩α=Q．
点评：本题考查了线面平行的性质、线面相交、平面的确定公理、反证法，考查了推理能力，属于中档题．
练习册系列答案
全能练考卷系列答案
相关题目
经统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系．对某小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如表：
由表中样本数据求得回归方程为
=
x+
，且直线l：x+18y=100上，则点（
，
）满足（ ）
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
 |
| y |
|
| b |
|
| a |
|
| a |
|
| b |
| A、在l左侧 | B、在l右侧 |
| C、在l上 | D、无法确定 |
一个圆锥的侧面展开图是中心角90°面积为S1的扇形，若圆锥的全面积是S2，则
=（ ）
| S1 |
| S2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
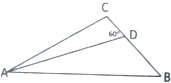爸爸去哪儿节目组安排星娃们露营，村长要求，Feyman、杨阳洋、贝儿依次在A、B、C三处扎篷．AB=8米，BC=4米，AC=6米．现村长给多多一个难题，要求她安扎在B、C两点之间的连线段的D处，且∠ADC=60°．问多多与Feyman相距
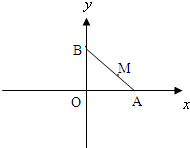如图，线段AB的两个端点A、B分别在x轴，y轴上滑动，|AB|=3，点M是线段AB上一点，且|AM|=1点M随线段AB的滑动而运动．