题目内容
用二项式定理证明:
(1)32n+2-8n-9能被64整除(n∈N);
(2)2n>n2(n≥5).
(1)32n+2-8n-9能被64整除(n∈N);
(2)2n>n2(n≥5).
考点:二项式定理的应用
专题:二项式定理
分析:(1)32n+2=9n+1=(8+1)n+1展开式中按照8的降幂排列,前边的项均能被64整除,最后两项为Cn+118+1=8n+9,与原式中的-8n-9抵消,分析可得答案.
(2)由于n-2≥3,由二项式定理可得2n-2>(n-1)+
,从而得到2n-n2=4•2n-2-n2>4[(n-1)+
]-n2=(n-3)2-1.根据函数f(n)=(n-3)2-1在(3,+∞)上单调递增,可得当n≥5时,f(n)≥f(5)=3>0,从而证得结论.
(2)由于n-2≥3,由二项式定理可得2n-2>(n-1)+
| (n-2)(n-3) |
| 2 |
| (n-2)(n-3) |
| 2 |
解答:
解:(1)证明:32n+2-8n-9=9n+1-8n-9=(8+1)n+1-8n-9
=8n+1+Cn+11•8n++Cn+1n•8+1-8n-9=8n+1+Cn+11•8n++Cn+1n-1•82 =82(8n-1+Cn+11•8n-2++Cn+1n-1),
∵8n-1+Cn+11•8n-2++Cn+1n-1是整数,∴32n+2-8n-9能被64整除.
(2)证明:∵n≥5,∴n-2≥3,
由二项式定理可得2n-2=(1+1)n-2=1+(n-2)+
+…+
>(n-1)+
.
∵2n-n2=4•2n-2-n2>4[(n-1)+
]-n2=n2-6n+8=(n-3)2-1.
由于函数f(n)=(n-3)2-1在(3,+∞)上单调递增,∴当n≥5时,f(n)≥f(5)=3>0,
∴n≥5时,2n>n2.
=8n+1+Cn+11•8n++Cn+1n•8+1-8n-9=8n+1+Cn+11•8n++Cn+1n-1•82 =82(8n-1+Cn+11•8n-2++Cn+1n-1),
∵8n-1+Cn+11•8n-2++Cn+1n-1是整数,∴32n+2-8n-9能被64整除.
(2)证明:∵n≥5,∴n-2≥3,
由二项式定理可得2n-2=(1+1)n-2=1+(n-2)+
| (n-2)(n-3) |
| 2 |
| C | n-2 n-2 |
| (n-2)(n-3) |
| 2 |
∵2n-n2=4•2n-2-n2>4[(n-1)+
| (n-2)(n-3) |
| 2 |
由于函数f(n)=(n-3)2-1在(3,+∞)上单调递增,∴当n≥5时,f(n)≥f(5)=3>0,
∴n≥5时,2n>n2.
点评:本题考查二项式定理的应用:处理整除问题,利用函数的单调性证明不等式,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
直线l1的倾斜角为30°,斜率为k1,直线l2过点(1,2),(5,2+
),斜率为k2,则( )
| 5 |
| A、k1>k2 |
| B、k1<k2 |
| C、k1=k2 |
| D、不能确定 |
已知数列{xn}满足xn+3=xn,xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1且a≠0),则数列{xn}的前2016项的和等于( )
| A、671 | B、760 |
| C、1324 | D、1344 |
 如图,过点D做圆的切线切于B点,作割线交圆于A,C两点,其中BD=3,AD=4,则AC=
如图,过点D做圆的切线切于B点,作割线交圆于A,C两点,其中BD=3,AD=4,则AC=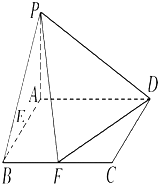 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.