题目内容
11.已知 p:方程x2+mx+1=0有两个不等的实根;q:方程4x2+4(m-2)x+1=0无实根.若“p”为假命题,“q”为真命题,求实数m的取值范围.分析 求出命题p:m>2,命题q:1<m<3,再由“p”为假命题,“q”为真命题,能求出m的取值范围.
解答 解:∵p:方程x2+mx+1=0有两个不相等的负实根,
∴$\left\{\begin{array}{l}{{m}^{2}-4>0}\\{m>0}\end{array}\right.$,∴m>2,
又∵q:方程4x2+4(m-2)x+1=0无实根,
∴△=4(m-2)2-4×4<0,
∴1<m<3,
∵“p”为假命题,“q”为真命题,
∴$\left\{\begin{array}{l}{m≤2}\\{1<m<3}\end{array}\right.$,∴1<m≤2.
∴m的取值范围是(1,2].
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意根的判别式及不等式性质的合理运用.

练习册系列答案
相关题目
19.以下命题正确的是( )
| A. | 经过空间中的三点,有且只有一个平面 | |
| B. | 空间中,如果两个角的两条边分别对应平行,那么这两个角相等 | |
| C. | 空间中,两条异面直线所成角的范围是(0,$\frac{π}{2}$] | |
| D. | 如果直线l平行于平面α内的无数条直线,则直线l平等于平面α |
3.设a=log30.3,b=20.3,c=0.32则( )
| A. | c>b>a | B. | c>a>b | C. | b>c>a | D. | b>a>c |
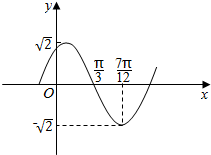 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$). 一个几何体的三视图如图所示,若其正视图、侧视图都是面积为$\frac{\sqrt{3}}{2}$,且一个角为60°的菱形,俯视图为正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$.
一个几何体的三视图如图所示,若其正视图、侧视图都是面积为$\frac{\sqrt{3}}{2}$,且一个角为60°的菱形,俯视图为正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$.