题目内容
已知p：1≤x≤2，q：
≤0，则p是q的 条件．（在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选择一个填写）
| x-2 |
| x-1 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据分式不等式的性质，结合充分条件和必要条件的定义，即可得到结论．
解答：
解：∵
≤0，
∴1＜x≤2，即q：1＜x≤2，
∵p：1≤x≤2，q：1＜x≤2，
∴p是q的必要不充分条件，
故答案为：必要不充分
| x-2 |
| x-1 |
∴1＜x≤2，即q：1＜x≤2，
∵p：1≤x≤2，q：1＜x≤2，
∴p是q的必要不充分条件，
故答案为：必要不充分
点评：本题主要考查充分条件和必要条件的判断，根据不等式的性质是解决本题的关键．
练习册系列答案
相关题目
定义在R上的奇函数f（x），当x＞0时，f（x）=x2-x-2函数f（x）的定义域为{x|x≠0}，f（x）＞0．满足f（x•y）=f（x）•f（y），且在区间（0，+∞）上单调递增，若实数a满足f（log2a）+f（log
a）≤2f（1），则a的取值范围是（ ）
| 1 |
| 2 |
| A、[1，2] | ||
B、（0，
| ||
C、[
| ||
| D、（0，1）∪（1，2] |
某扇形的圆心角为30°，半径为2，那么该扇形弧长为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、60 |
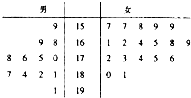某县职工运动会将在本县一中运动场隆重召开，为了搞好接待工作，执委会在一中招募了12名男性志愿者和18名女性志愿者，调查发现，这30名志愿者的身高如图：（单位：cm）