题目内容
已知三棱锥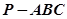 中,
中, ,
,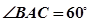 ,
,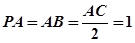 ,
,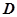 ,
,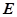 分别是
分别是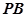 ,
,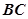 中点.
中点.
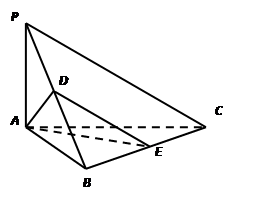
(1)求证: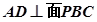 ;
;
(2)求直线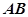 与平面
与平面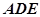 所成角的正弦值.
所成角的正弦值.
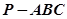 中,
中, ,
,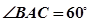 ,
,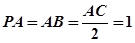 ,
,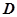 ,
,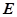 分别是
分别是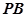 ,
,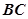 中点.
中点.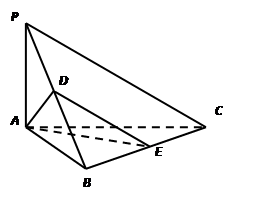
(1)求证:
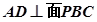 ;
;(2)求直线
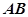 与平面
与平面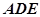 所成角的正弦值.
所成角的正弦值.(1)见解析 (2)

(1)由条件知: ,
,
∵
∴ ,
,
又∵ 且
且
∴
又∵
∴
又∵ 且
且
∴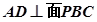
(2)作 于点
于点

由(1)知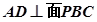 ,则
,则
故 ,则
,则 是直线
是直线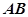 与平面
与平面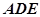 所成角
所成角

在 △
△ 中,
中, ,
, ,
,
由面积法 ,得
,得
直线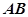 与平面
与平面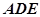 所成角的正弦值为
所成角的正弦值为
 ,
,
∵

∴
 ,
,又∵
 且
且
∴

又∵

∴

又∵
 且
且
∴
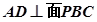
(2)作
 于点
于点

由(1)知
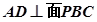 ,则
,则
故
 ,则
,则 是直线
是直线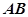 与平面
与平面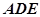 所成角
所成角
在
 △
△ 中,
中, ,
, ,
,
由面积法
 ,得
,得
直线
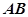 与平面
与平面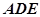 所成角的正弦值为
所成角的正弦值为

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
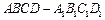 中,点
中,点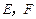 分别在
分别在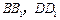 上,且
上,且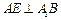 ,
,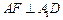 .
.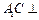 平面
平面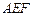 ;
;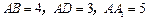 时,求平面
时,求平面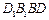 所成角的大小.
所成角的大小.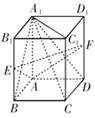

 中,
中, 分别为棱
分别为棱 的中点,已知
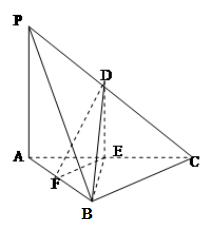
的中点,已知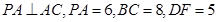 ,
,
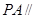 平面
平面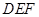 ;
;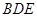
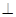 平面
平面 .
.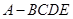 中,平面
中,平面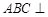 平面
平面 ;
;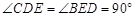 ,
, ,
,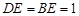 ,
,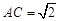 .
.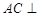 平面
平面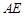 与平面
与平面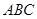 所成的角的正切值.
所成的角的正切值.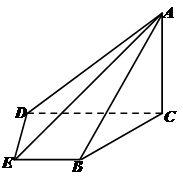
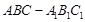 中,
中, 底面
底面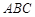 ,
,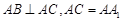 ,E、F分别是棱
,E、F分别是棱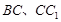 的中点.
的中点.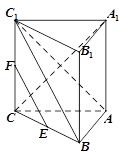
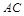 上的点
上的点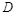 满足平面
满足平面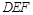 //平面
//平面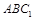 ,试确定点
,试确定点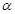 、
、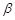 、
、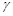 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ).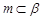 ,
,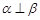 ,则
,则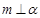
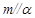 ,
,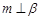 ,则
,则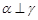 ,则
,则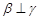
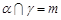 ,
,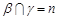 ,
,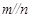 ,则
,则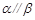
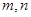 是不同的直线,
是不同的直线,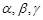 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: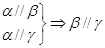 ②
②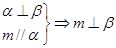
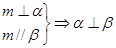 ④
④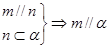
 ,
, 与平面
与平面 ,
, ,
, ,满足
,满足 ,
, ,
, ,
, ,则必有( )
,则必有( ) 且
且
 且
且