题目内容
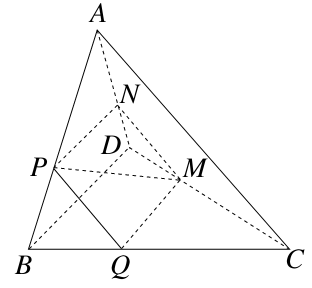
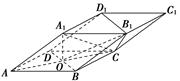
如图,在四棱锥 中,平面
中,平面 平面
平面 ;
; ,
, ,
,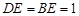 ,
,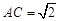 .
.
(1)证明: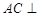 平面
平面 ;
;
(2)求直线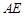 与平面
与平面 所成的角的正切值.
所成的角的正切值.
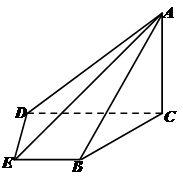
 中,平面
中,平面 平面
平面 ;
;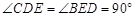 ,
, ,
,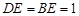 ,
,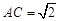 .
.(1)证明:
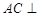 平面
平面 ;
;(2)求直线
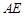 与平面
与平面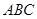 所成的角的正切值.
所成的角的正切值.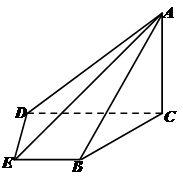
(1)详见解析;(2) .
.
 .
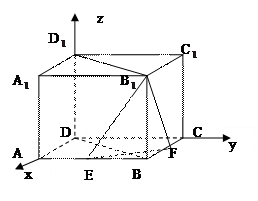
.试题分析:(1)连结
 ,在直角梯形
,在直角梯形 中,由勾股定理证明
中,由勾股定理证明 ,再证平面
,再证平面 平面
平面 ,从而
,从而 平面
平面 ;(2)在直角梯形
;(2)在直角梯形 中,证明
中,证明 ,再证
,再证 平面
平面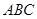 .
.作
 于
于 的延长线交于
的延长线交于 ,连结
,连结 ,证明
,证明 平面
平面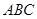 ,从而可得
,从而可得 是直线
是直线 与平面
与平面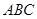 所成的角.在
所成的角.在 中,求
中,求 ,在
,在 中,求
中,求 ,在
,在 中,求
中,求 ,
,即得直线
 与平面
与平面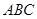 所成的角的正切值.
所成的角的正切值.(1)连结
 ,在直角梯形
,在直角梯形 中,由
中,由 ,
, 得
得 ,
,由
 得
得 ,即
,即 ,
,又平面
 平面
平面 ,从而
,从而 平面
平面 .
.(2)在直角梯形
 中,由
中,由 ,
, 得
得 ,
,又平面
 平面
平面 ,所以
,所以 平面
平面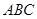 .
.作
 于
于 的延长线交于
的延长线交于 ,连结
,连结 ,则
,则 平面
平面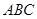 ,
,所以
 是直线
是直线 与平面
与平面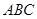 所成的角.
所成的角.在
 中,由
中,由 ,
, ,得
,得 ,
, ,
,在
 中,
中, ,
, ,得
,得 ,
,在
 中,由
中,由 ,
, 得
得 ,
,所以直线
 与平面
与平面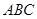 所成的角的正切值是
所成的角的正切值是 .
.
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.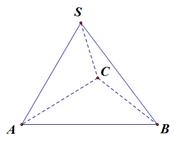
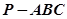 中,
中, ,
,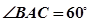 ,
,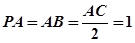 ,
, ,
,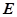 分别是
分别是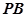 ,
,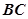 中点.
中点.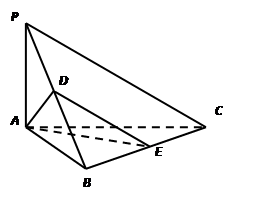
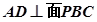 ;
;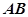 与平面
与平面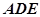 所成角的正弦值.
所成角的正弦值.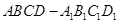 中,底面
中,底面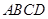 是等腰梯形,
是等腰梯形,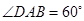 ,
,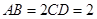 ,
,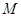 是线段
是线段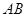 的中点.
的中点.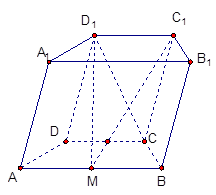
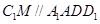 ;
;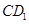 垂直于平面
垂直于平面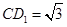 ,求平面
,求平面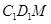 和平面
和平面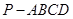 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱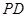 ⊥底面
⊥底面  ,
,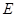 是
是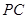 的中点,作
的中点,作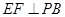 交
交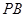 于点
于点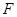 .
.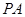
 平面
平面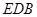 ;
;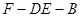 的正弦值.
的正弦值. 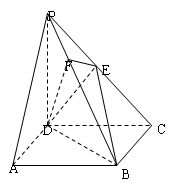
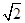 .
.
 B
B ,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D
,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D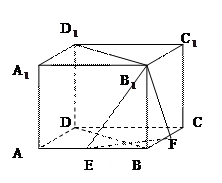
 ,则
,则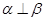 ;②若
;②若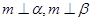 ,则
,则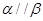 ;③若
;③若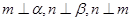 ,则
,则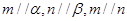 ,则
,则