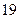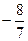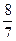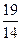题目内容
设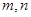 是不同的直线,
是不同的直线,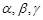 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①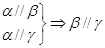 ②
②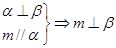
③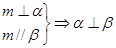 ④
④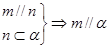
其中,真命题是( )
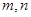 是不同的直线,
是不同的直线,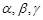 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:①
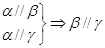 ②
②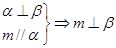
③
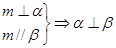 ④
④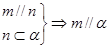
其中,真命题是( )
| A.①④ | B.②③ | C.①③ | D.②④ |
C.
试题分析:对于①利用平面与平面平行的性质定理可证
 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ,正确;对于②面
,正确;对于②面 ⊥面
⊥面 ,
, ∥面
∥面 ,此时
,此时 ∥面
∥面 ,不正确;对应③因为
,不正确;对应③因为 ∥
∥ ,所以
,所以 内有一直线与
内有一直线与 平行,而
平行,而 ,根据面面垂直的判定定理可知
,根据面面垂直的判定定理可知 ,故正确;对应④
,故正确;对应④ 有可能在平面
有可能在平面 内,故不正确. 故选D.
内,故不正确. 故选D.
练习册系列答案
相关题目
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.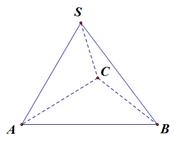
 中,
中, 、
、 分别为
分别为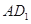 ,
,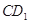 中点。
中点。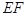 与
与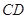 所成角的大小;
所成角的大小;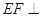 平面
平面 。
。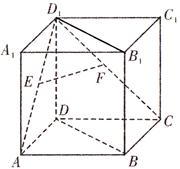
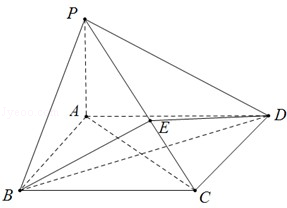
 中,
中, ,
,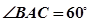 ,
,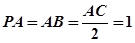 ,
, ,
, 分别是
分别是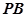 ,
,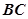 中点.
中点.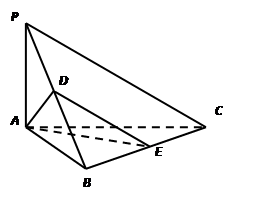
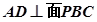 ;
;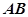 与平面
与平面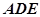 所成角的正弦值.
所成角的正弦值.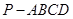 中,底面
中,底面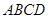 是正方形,侧棱
是正方形,侧棱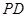 ⊥底面
⊥底面  ,
,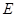 是
是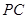 的中点,作
的中点,作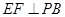 交
交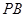 于点
于点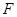 .
.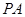
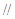 平面
平面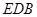 ;
;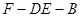 的正弦值.
的正弦值. 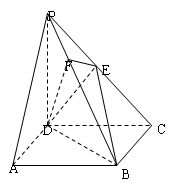
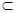 α,n∥α,则m∥n
α,n∥α,则m∥n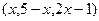 ,B
,B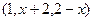 ,当
,当 取最小值时,
取最小值时,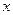 的值等于( )
的值等于( )