题目内容
8.若函数f(x)=$\left\{\begin{array}{l}{{e}^{x}+1,x<1}\\{f(lnx),x≥1}\end{array}\right.$,则f(e)=( )| A. | 0 | B. | 1 | C. | 2 | D. | e+1 |
分析 根据函数f(x)的解析式,求出f(e)=f(0),求出函数值即可.
解答 解:∵e>1,f(x)=$\left\{\begin{array}{l}{{e}^{x}+1,x<1}\\{f(lnx),x≥1}\end{array}\right.$,
∴f(e)=f(lne)=f(1)=f(ln1)=f(0)=e0+1=2,
故选:C.
点评 本题考查了求函数的定义域问题,考查函数求值问题,是一道基础题.

练习册系列答案
相关题目
13.若g(x)=2x-1,f[g(x)]=$\frac{1+{x}^{2}}{3{x}^{2}}$,则f(-3)=( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
18.下列说法正确的是( )
| A. | 若“x=$\frac{π}{4}$,则tanx=1”的逆命题为真命题 | |
| B. | 在△ABC中,sinA>sinB的充要条件是A>B | |
| C. | 函数f(x)=sinx+$\frac{4}{sinx}$,x∈(0,π)的最小值为4 | |
| D. | ?x∈R,使得sinx•cosx=$\frac{3}{5}$ |
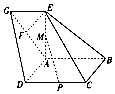 如图,四边形ABCD是正方形,且平面ABCD⊥平面ABEG,F是AG上一点,且△ABE与△AEF都是等腰直角三角形,AB=AE,AF=EF.
如图,四边形ABCD是正方形,且平面ABCD⊥平面ABEG,F是AG上一点,且△ABE与△AEF都是等腰直角三角形,AB=AE,AF=EF.