题目内容
10.数列{an}满足a1=$\frac{4}{3},{a_{n+1}}-1={a_n}({a_n}-1),n∈{N^*}$且Sn=$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}$,则Sn的整数部分的所有可能值构成的集合是{0,1,2}.分析 数列{an}满足a1=$\frac{4}{3}$,an+1-1=an(an-1)(n∈N*).可得:an+1-an=(an-1)2>0,可得:数列{an}单调递增.可得a2=$\frac{13}{9}$,a3=$\frac{133}{81}$,a4=$\frac{13477}{6561}$,$\frac{1}{{a}_{3}-1}$=$\frac{81}{52}$>1,$\frac{1}{{a}_{4}-1}$=$\frac{6561}{6916}$<1.另一方面:$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$,可得Sn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$…+$\frac{1}{{a}_{n}}$=($\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{2}-1}$)+($\frac{1}{{a}_{2}-1}$-$\frac{1}{{a}_{3}-1}$)+…+($\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$)=3-$\frac{1}{{a}_{n+1}-1}$,对n=1,2,3,n≥4,分类讨论即可得出.
解答 解:∵数列{an}满足a1=$\frac{4}{3}$,an+1-1=an(an-1)(n∈N*).
可得:an+1-an=(an-1)2>0,∴an+1>an,因此数列{an}单调递增.
则a2-1=$\frac{4}{3}$,可得a2=$\frac{13}{9}$,同理可得:a3=$\frac{133}{81}$,a4=$\frac{13477}{6561}$.$\frac{1}{{a}_{3}-1}$=$\frac{81}{52}$>1,
$\frac{1}{{a}_{4}-1}$=$\frac{6561}{6916}$<1,
另一方面:$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$,
∴Sn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$…+$\frac{1}{{a}_{n}}$=($\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{2}-1}$)+($\frac{1}{{a}_{2}-1}$-$\frac{1}{{a}_{3}-1}$)+…+($\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$)
=$\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{n+1}-1}$=3-$\frac{1}{{a}_{n+1}-1}$,
当n=1时,S1=$\frac{1}{{a}_{1}}$=$\frac{3}{4}$,其整数部分为0;
当n=2时,S2=$\frac{3}{4}$+$\frac{9}{13}$=1+$\frac{23}{52}$,其整数部分为1;
当n=3时,S3=$\frac{3}{4}$+$\frac{9}{13}$+$\frac{81}{133}$=2+$\frac{355}{6561}$,其整数部分为2;
当n≥4时,Sn=2+1-$\frac{1}{{a}_{n+1}-1}$∈(2,3),其整数部分为2.
综上可得:Sn的整数部分的所有可能值构成的集合是{0,1,2}.
故答案为:{0,1,2}.
点评 本题考查了数列的单调性、递推关系、“裂项求和”方法,考查了分类讨论方法、推理能力与计算能力,属于难题.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | f(5)<f(2)<f(-1) | B. | f(2)<f(5)<f(-1) | C. | f(-1)<f(2)<f(5) | D. | f(2)<f(-1)<f(5) |
| A. | $-2\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | -4 | D. | 4 |
| A. | y=x+1 | B. | $y={log_{\frac{1}{2}}}x$ | C. | y=2x | D. | y=-(x-1)2 |

 的奇偶性;
的奇偶性; ,函数
,函数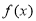 在区间
在区间 上为减函数,求实数a的取值范围.
上为减函数,求实数a的取值范围.