题目内容
5.设a、b>0,a+b=5,则$\sqrt{a+1}$+$\sqrt{b+3}$的取值范围为(1+2$\sqrt{2}$,3$\sqrt{2}$].分析 令y=$\sqrt{a+1}$+$\sqrt{b+3}$,则y2=($\sqrt{a+1}$+$\sqrt{b+3}$)2=9+2$\sqrt{ab+b+3a+3}$=9+2$\sqrt{-{a}^{2}+7a+8}$,利用配方法能求出$\sqrt{a+1}$+$\sqrt{b+3}$的取值范围.
解答 解:令y=$\sqrt{a+1}$+$\sqrt{b+3}$,
则y2=($\sqrt{a+1}$+$\sqrt{b+3}$)2=a+1+b+3+2$\sqrt{(a+1)(b+3)}$
=9+2$\sqrt{ab+b+3a+3}$
=9+2$\sqrt{-{a}^{2}+7a+8}$
=9+2$\sqrt{-(a-\frac{7}{2})^{2}+\frac{81}{4}}$,
∴当a=$\frac{7}{2}$时,ymax=$\sqrt{9+2\sqrt{\frac{81}{4}}}$=3$\sqrt{2}$,
当a→0时,ymin→$\sqrt{9+2\sqrt{-\frac{49}{4}+\frac{81}{4}}}$=$\sqrt{9+4\sqrt{2}}$=$\sqrt{(1+2\sqrt{2})^{2}}$=1+2$\sqrt{2}$,
∴$\sqrt{a+1}$+$\sqrt{b+3}$的取值范围为(1+2$\sqrt{2}$,3$\sqrt{2}$].
故答案为:(1+2$\sqrt{2}$,3$\sqrt{2}$].
点评 本题考查函数的取值范围的求法,是中档题,解题时要认真审题,注意配方法的合理运用.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
1.已知数列{an}满足a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,Sn是其前n项和,则S2015=( )
| A. | $\frac{2011}{2}$ | B. | 1009 | C. | 1007 | D. | $\frac{2017}{2}$ |
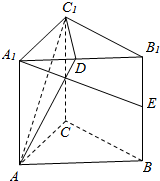 如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.
如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.