题目内容

20．已知定义在R上的函数f（x），对任意x1，x2∈R．且x1≠x2．总有（x1-x2）[f（x1）-f（x2）]＞0，且函数f（x） 的图象经过点A（5，-2）．若f（2m-1）＜-2．求m的取值范围．

分析 先求出函数的单调性，得到2m-1＜5，解出即可．

解答 解：∵（x1-x2）[f（x1）-f（x2）]＞0，
∴x1＞x2时：f（x1）＞f（x2），
x1＜x2时：f（x1）＜f（x2），
∴函数f（x）在R上递增，
∵f（5）=-2，
∴由f（2m-1）＜-2=f（5），
得：2m-1＜5，解得：m＜3．

点评 本题考查了函数的单调性问题，是一道基础题．

练习册系列答案
相关题目
10．二次函数f（x）的图象过点为A（-1，-16），且f（x）≤0的解集为{x|-5≤x≤3}，g（x）=2x2+ax+1．
（1）求函数f（x）的解析式；
（2）解不等式g（x）≥0；
（3）若不等式xf（x）≥g（x）在区间x∈[1，2]上恒成立，求实数a的取值范围．
11．设f（x）是定义在（0，+∞）上的单调增函数，且满足f（xy）=f（x）+f（y），f（3）=1．
（1）求f（1）；
（2）若f（x）+2≤f（x+8），求x的取值范围．
8．计算下列各式（式中字母都是正数）：（0.0081）${\;}^{-\frac{1}{4}}$-[3×（$\frac{7}{8}$）0]-1．
15．已知sinθ=$\frac{m-3}{m+5}$，cosθ=$\frac{4-2m}{m+5}$，则tan（kπ+θ）（k∈Z）的值为（　　）
A．$\frac{4-2m}{m-3}$B．±$\frac{m-3}{4-2m}$C．-$\frac{5}{12}$D．-$\frac{3}{4}$或-$\frac{5}{12}$
5．设a、b＞0，a+b=5，则$\sqrt{a+1}$+$\sqrt{b+3}$的取值范围为（1+2$\sqrt{2}$，3$\sqrt{2}$]．
12．在△ABC中，已知cosA=$\frac{3}{5}$，tanB=2，则cosC的值为（　　）
A．$\frac{11\sqrt{5}}{25}$B．$\frac{\sqrt{5}}{5}$C．-$\frac{\sqrt{5}}{5}$D．-$\frac{11\sqrt{5}}{25}$
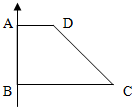15．如图1，直角梯形ABCD中，∠A=∠B=90°，AD∥BC，AD=2，AB=3，BC=6，把直角梯形ABCD绕边AB旋转一周得到一个旋转体，求：
（1）旋转体的表面积，
（2）旋转体的体积．
16．下列命题：
①如果函数f（x）对任意的x∈R，都有f（a+x）=f（a-x）（a为常数），那么函数f（x）必为偶函数；
②如果函数f（x）对任意的x∈R，满足f（x+2）=-f（x），那么函数f（x）是周期函数；
③如果函数f（x）对任意x1，x2∈R，且x1≠x2，都有（x1-x2）[f（x1）-f（x2）]＞0，那么f（x）在R上是增函数；
④函数y=f（x）和函数y=f（x-1）+2的图象一定不会重合．
其中真命题的序号是②③．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网