题目内容
17．设函数f（x）=$\left\{\begin{array}{l}{1+lo{g}_{2}（2-x），x＜1}\\{{2}^{x-1}，x＞1}\end{array}\right.$，则f（f（-2））=（ ）| A． | 3 | B． | 4 | C． | 8 | D． | $\frac{1}{8}$ |
分析 由已知中函数f（x）=$\left\{\begin{array}{l}{1+lo{g}_{2}（2-x），x＜1}\\{{2}^{x-1}，x＞1}\end{array}\right.$，将x=-2代入可得答案．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{1+lo{g}_{2}（2-x），x＜1}\\{{2}^{x-1}，x＞1}\end{array}\right.$，
∴f（-2）=3．
∴f（f（-2））=f（3）=4．
故选：B
点评 本题考查的知识点是分段函数的应用，函数求值，难度不大，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．复数z=$\frac{3-2{i}^{3}}{1+i}$的虚部为（ ）
| A． | -$\frac{1}{2}$ | B． | -1 | C． | $\frac{5}{2}$ | D． | $\frac{1}{2}$ |
8．圆x2+y2+2x-6y+1=0关于直线ax-by+3=0（a＞0，b＞0）对称，则$\frac{1}{a}$$+\frac{3}{b}$的最小值是（ ）
| A． | 2$\sqrt{3}$ | B． | $\frac{20}{3}$ | C． | 4 | D． | $\frac{16}{3}$ |
12．已知集合M={1，3，4}，N={x|x2-4x+3=0}，则M∩N=（ ）
| A． | {3，4} | B． | {1，4} | C． | {1，3} | D． | {3} |
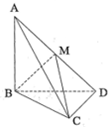如图，三棱锥A-BCD中，AB⊥平面BCD，CD⊥BD．
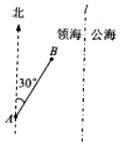一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击，已知缉私艇的最大航速是走私船最大航速的3倍，假设缉私艇和走私船均按直线方向以最大航速航行．