题目内容
10.已知不过坐标原点的动直线l与抛物线y2=4x交于P,Q两点,若以PQ为直径的圆横过坐标原点O,则直线l在x轴上的截距为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设直线l:x=my+b,代入抛物线y2=4x,利用韦达定理及向量数量积公式即可得到结论.
解答 解:设直线l:x=my+b,(b≠0),代入抛物线y2=4x,可得y2-4my-4b=0.
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4b,
∴x1x2=(my1+b)(my2+b)=b2,
∵OA⊥OB,∴x1x2+y1y2=0,
可得b2-4b=0,
∵b≠0,∴b=4,∴直线l:x=my+4,
令y=0,可得x=4.
故选D.
点评 本题考查直线与抛物线的位置关系,考查向量知识的运用,正确运用韦达定理是关键.

练习册系列答案
相关题目
17.设函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),x<1}\\{{2}^{x-1},x>1}\end{array}\right.$,则f(f(-2))=( )
| A. | 3 | B. | 4 | C. | 8 | D. | $\frac{1}{8}$ |
15.设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( )
| A. | 1+a,4 | B. | 1+a,4+a | C. | 1,4 | D. | 1,4+a |
19.随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,如图是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面叙述不正确的是( )
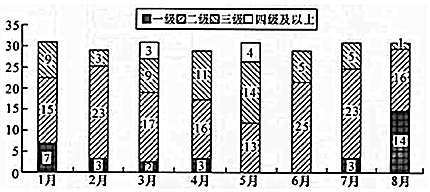

| A. | 1月至8月空气合格天数超过20天的月份有5个 | |
| B. | 第二季度与第一季度相比,空气达标天数的比重下降了 | |
| C. | 8月是空气质量最好的一个月 | |
| D. | 6月份的空气质量最差 |
20.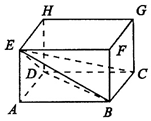 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |