题目内容
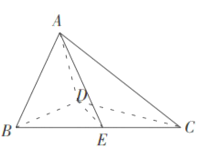
【题目】已知长方体
中， 
为
的中点， 
在棱
上， 
， 
.
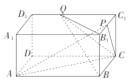
（1）若异面直线
与
互相垂直，求
的长；
（2）当四棱锥
的体积为
时，求证：直线
平面
.
【答案】（1）
；（2）见解析.
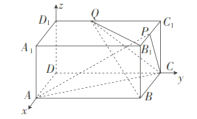
【解析】试题分析：如图，以
为原点，分别以
所在的直线为
轴、
轴、
轴建立空间直角坐标系.得到相应点和相应向量的坐标，利用空间向量的夹角公式可得
的长
（2）证明：因为
是长方体， 
在棱
上，所以
平面
，
所以四棱锥
的体积
，解得
.
此时
为
的中点，所以
. 利用空间向量的知识可证得直线
平面
..
试题解析：（1）如图，以
为原点，分别以
所在的直线为
轴、
轴、
轴建立空间直角坐标系.
则
， 
， 
， 
， 
， 
， 
.
设
，则
， 
，
因为
，所以
，即
，解得
.
所以，当异面直线
与
互相垂直时， 
.
（2）证明：因为
是长方体， 
在棱
上，所以
平面
，
所以四棱锥
的体积
，解得
.
此时
为
的中点，所以
.
由（1）可知
， 
， 
.
设平面
的法向量为
，则
，即
，
令
，得
， 
，所以
，
因为
，
所以
，因为直线
平面
，
所以直线
平面
.
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限
（年）和所支出的维修费用
（万元）有如下统计资料：
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知， 
对
呈线性相关关系，试求：
（1）回归直线方程；
（2）估计使用年限为10年时，维修费用约是多少？
参考公式：回归直线方程： 
.其中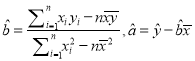
（注： 
)
