题目内容
1.已知数列$\frac{1}{1×3}$,$\frac{1}{3×5}$,$\frac{1}{5×7}$,…,$\frac{1}{(2n-1)(2n+1)}$的前n项和Sn(1)计算S1,S2,S3,S4;并由此推测Sn的表达式;
(2)证明(1)中推测的结论.
分析 (1)利用Sn=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$,分别取n=1,2,3,4即可得出.
(2)利用“裂项求和”方法即可证明.
解答 解:(1)Sn=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$,
S1=$\frac{1}{3}$,
S2=$\frac{1}{3}+\frac{1}{3×5}$=$\frac{2}{5}$,
同理可得:
S3=$\frac{3}{7}$,
S4=$\frac{4}{9}$.
由此推测Sn=$\frac{n}{2n+1}$.
证明:(2)∵$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$.
∴Sn=$\frac{1}{2}$$[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
点评 本题考查了数列递推关系、“裂项求和”方法、数列通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
9.设X~B(4,p),其中0<p<$\frac{1}{2}$,且P(X=2)=$\frac{8}{27}$,那么P(X=1)=( )
| A. | $\frac{8}{81}$ | B. | $\frac{16}{81}$ | C. | $\frac{8}{27}$ | D. | $\frac{32}{81}$ |
16.复数z满足|z-3i|=10,则复平面内和复数z对应的点围成的几何图形是( )
| A. | 椭圆 | B. | 双曲线 | C. | 圆 | D. | 抛物线 |
11.函数f(x)的图象如图所示,则下列关系正确的是( )
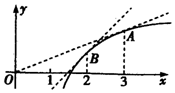

| A. | 0<f'(2)<f'(3)<f(3)-f(2) | B. | 0<f'(2)<f(3)-f(2)<f'(3) | C. | 0<f'(3)<f(3)-f(2)<f'(2) | D. | 0<f(3)-f(2)<f'(2)-f'(3) |