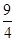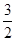题目内容
设数列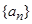 的前
的前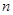 项和为
项和为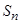 ,对任意
,对任意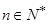 满足
满足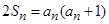 ,且
,且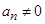 .
.
(Ⅰ)求数列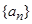 的通项公式;
的通项公式;
(Ⅱ)设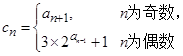 ,求数列
,求数列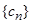 的前
的前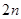 项和
项和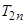 .
.
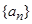 的前
的前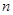 项和为
项和为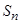 ,对任意
,对任意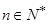 满足
满足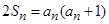 ,且
,且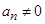 .
.(Ⅰ)求数列
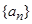 的通项公式;
的通项公式;(Ⅱ)设
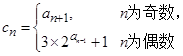 ,求数列
,求数列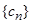 的前
的前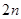 项和
项和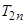 .
.(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;
;
 ;(Ⅱ)
;(Ⅱ) ;
;(Ⅰ)对条件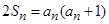 进行变形得出数列满足的递推关系,进而再求通项公式;(Ⅱ)对
进行变形得出数列满足的递推关系,进而再求通项公式;(Ⅱ)对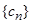 的前
的前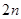 项进行分组求和,转化为等差数列和等比数列求和.
项进行分组求和,转化为等差数列和等比数列求和.
试题分析:
试题解析:(Ⅰ) ,①
,①
 当
当 时,
时, ,②
,②
以上两式相减得 , 2分
, 2分
即 ,
,
 ,
, 当
当 时,有
时,有 . 5分
. 5分
又当 时,由
时,由 及
及 得
得 ,
,
所以数列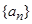 是等差数列,其通项公式为
是等差数列,其通项公式为 . 8分
. 8分
(Ⅱ)由(Ⅰ)得 . 9分
. 9分
所以 10分
10分

 . 14分
. 14分
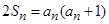 进行变形得出数列满足的递推关系,进而再求通项公式;(Ⅱ)对
进行变形得出数列满足的递推关系,进而再求通项公式;(Ⅱ)对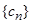 的前
的前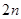 项进行分组求和,转化为等差数列和等比数列求和.
项进行分组求和,转化为等差数列和等比数列求和.试题分析:
试题解析:(Ⅰ)
 ,①
,① 当
当 时,
时, ,②
,②以上两式相减得
 , 2分
, 2分即
 ,
,  ,
, 当
当 时,有
时,有 . 5分
. 5分又当
 时,由
时,由 及
及 得
得 ,
,所以数列
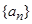 是等差数列,其通项公式为
是等差数列,其通项公式为 . 8分
. 8分(Ⅱ)由(Ⅰ)得
 . 9分
. 9分所以
 10分
10分
 . 14分
. 14分
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
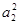 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,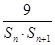 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.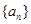 的前
的前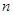 项和为
项和为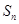 ,且
,且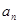 是
是 的等差中项,等差数列
的等差中项,等差数列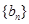 满足
满足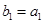 ,
,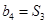 .
.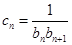 ,数列
,数列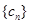 的前
的前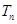 ,证明:
,证明: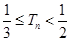 .
.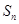 为数列
为数列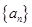 的前
的前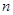 项和,对任意的
项和,对任意的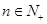 ,都有
,都有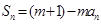 (
(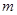 为正常数).
为正常数).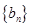 满足
满足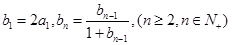 求数列
求数列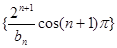 的前
的前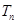 .
. 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, 满足
满足 ,求数列
,求数列 .
. 中,
中, ,前n项和
,前n项和 ,其中a、b、c为常数,则
,其中a、b、c为常数,则 ( )
( )



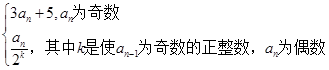
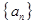 中,
中,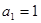 ,
,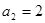 ,若
,若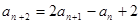 ,则
,则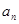 等于( )
等于( )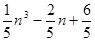
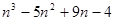
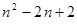
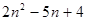
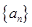 的前项和为
的前项和为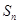 ,且
,且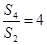 ,则
,则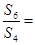 ( )
( )