题目内容
12．将编号1，2，3，4，5的小球放入编号1，2，3，4，5的盒子中，每个盒子放一个小球，则至多有两个小球的编号与盒子的编号相同的放法共有109种．分析 利用间接法，由分步计数原理计算可得答案．
解答 解：5个球全排列为A55=120种情况
3个球的编号与盒子的相同，先选出3个小球，放到对应序号的盒子里，有C53=10种情况，另外2个球，有1种不同的放法，故10种情况
5个球的编号与盒子的相同，有1种不同的放法，
故至多有两个小球的编号与盒子的编号相同的放法共有120-10-1=109种不同的放法，
故答案为：109．
点评 本题考查两个计数原理的综合运用，解题的关键在于求出3个球的编号与盒子的相同情况．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
2．不等式|x2-2|＜2的解集是（ ）
| A． | （-2，0）∪（0，2） | B． | （-2，2） | C． | （-1，0）∪（0，1） | D． | （-1，1） |
3．曲线y=$\frac{x}{x+1}$+lnx在点（1，$\frac{1}{2}$）处的切线方程为（ ）
| A． | y=$\frac{5}{4}$x+$\frac{3}{4}$ | B． | y=$\frac{5}{4}$x-$\frac{3}{4}$ | C． | y=-$\frac{5}{4}$x-$\frac{3}{4}$ | D． | y=-$\frac{5}{4}$x+$\frac{3}{4}$ |
7．已知椭圆和双曲线有共同的焦点F1，F2，P是它们的一个交点，且∠F1PF2=$\frac{π}{3}$，记椭圆和双曲线的离心率分别为e1，e2，则当e1e2取最小值时，e1，e2分别为（ ）
| A． | $\frac{1}{2}$，$\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{3}}{3}$，$\frac{\sqrt{6}}{2}$ | C． | $\frac{\sqrt{2}}{2}$，$\frac{\sqrt{6}}{2}$ | D． | $\frac{\sqrt{2}}{4}$，$\sqrt{3}$ |
4．下列函数中，y的最小值为4的是（ ）
| A． | y=x+$\frac{4}{x}$ | B． | y=$\frac{2（x+3）}{\sqrt{{x}^{2}+2}}$ | ||
| C． | y=sin x+$\frac{4}{sinx}$（0＜x＜π） | D． | y=ex+e-x |
1．已知双曲线$\frac{{x}^{2}}{（m+1）^{2}}$-$\frac{{y}^{2}}{{m}^{2}}$=1（m＞0）的离心率为$\frac{{\sqrt{5}}}{2}$，P是该双曲线上的点，P在该双曲线两渐近线上的射影分别是A，B，则|PA|•|PB|的值为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
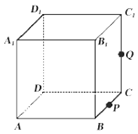如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．